分析:需先求函数f(x)的解析式,再由f′(x)≥0在(-1,1)上恒成立,即可求出t的取值范围.
解法一:依定义f(x)=x2(1-x)+t(x+1)=-x3+x2+tx+t,
则f′(x)=-3x2+2x+t.
若f(x)在(-1,1)上是增函数,则在(-1,1)上可设f′(x)≥0.
∴f′(x)≥0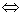 t≥3x2-2x在区间(-1,1)上恒成立.
t≥3x2-2x在区间(-1,1)上恒成立.
考虑函数g(x)=3x2-2x,由于g(x)的图象是对称轴为x=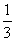 ,开口向上的抛物线,故要使t≥3x2-2x在区间(-1,1)上恒成立
,开口向上的抛物线,故要使t≥3x2-2x在区间(-1,1)上恒成立 t≥g(-1),即t≥5.
t≥g(-1),即t≥5.
而当t≥5时,f(x)在(-1,1)上满足f(x)>0,即f(x)在(-1,1)上是增函数.
故t的取值范围是t≥5.
解法二:依定义f(x)=x2(1-x)+t(x+1)=-x3+x2+tx+t.
f′(x)=-3x2+2x+t.
若f(x)在(-1,1)上是增函数.则在(-1,1)上可设f′(x)≥0
∵f(x)的图象是开口向下的抛物线.
∴当且仅f(1)=t-1≥0,且f(-1)=t-5≥0时,f(x)在(-1,1)上满足f(x)>0,即f(x)在(-1,1)上是增函数.
故t的取值范围是t≥5.

![]() t≥3x2-2x在区间(-1,1)上恒成立.
t≥3x2-2x在区间(-1,1)上恒成立.![]() ,开口向上的抛物线,故要使t≥3x2-2x在区间(-1,1)上恒成立
,开口向上的抛物线,故要使t≥3x2-2x在区间(-1,1)上恒成立![]() t≥g(-1),即t≥5.
t≥g(-1),即t≥5.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案