
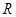 上的函数
上的函数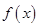 满足
满足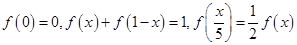 且当
且当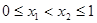 时,
时,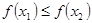 ,则
,则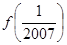 等于
等于A. | B. | C. | D. |
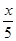 )=
)= f(x),∴当x=1时,f(
f(x),∴当x=1时,f(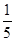 )=
)= f(1)=
f(1)= ;
;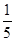 ,由f(
,由f(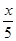 )=
)= f(x)得:
f(x)得: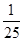 )=
)= f(
f(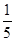 )=
)=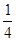 ;同理可求:f(
;同理可求:f(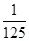 )=
)= f(
f(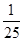 )=
)=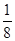 ;
;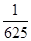 )=)=
)=)= f(
f(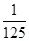 )=
)=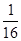 ;
;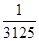 )=
)= f(
f(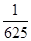 )=
)=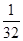 ①
① ,由f(x)+f(1-x)=1,可求得f(
,由f(x)+f(1-x)=1,可求得f( )=
)= ,
, )+f(1-
)+f(1- )=1,解得f(
)=1,解得f( )=
)= ,
, ,同理反复利用f(
,同理反复利用f(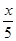 )=
)= f(x),
f(x),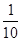 )=)=
)=)= f(
f( )=
)=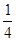 ;
;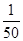 )=
)= f(
f(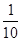 )=
)=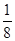 ;…
;…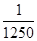 )=
)= f(
f(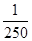 )=
)=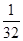 ②
②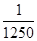 )=f(
)=f(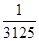 )=
)=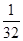 ,
,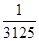 <
<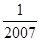 <
<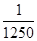 <1
<1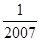 )≥f(
)≥f(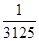 )=
)=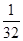 ,
,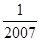 )≤f(
)≤f(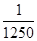 )=
)=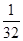 ;
;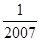 )=
)=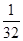 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 ,
, 在区间(0,1]上恒成立,试求b的取值范围。
在区间(0,1]上恒成立,试求b的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
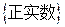 ,
,
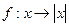 是从A到B的映射;
是从A到B的映射;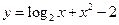 在
在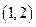 内有一个零点;
内有一个零点;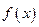 是奇函数,函数
是奇函数,函数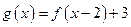 ,则
,则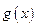 图像的对称中心的坐标
图像的对称中心的坐标 是
是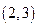 ;
;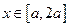 ,都有
,都有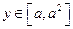 ,且
,且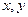 满足方程
满足方程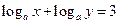 ,这时
,这时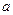 的取值集合为
的取值集合为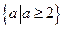 .其中正确的结论序号是
.其中正确的结论序号是 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com