
(本题满分6分)
求不等式 
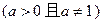 中的
中的 的取
的取 值范围.
值范围.
科目:高中数学 来源:2011-2012学年上海市青浦区高三上学期期终学习质量调研测试数学试卷 题型:解答题
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设 ,对于项数为
,对于项数为 的有穷数列
的有穷数列 ,令
,令 为
为 中最大值,称数列
中最大值,称数列 为
为 的“创新数列”.例如数列
的“创新数列”.例如数列 3,5,4,7的创新数列为3,5,5,7.
3,5,4,7的创新数列为3,5,5,7.
考查自然数 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列 .
.
(1)若 ,写出创新数列为3,4,4,4的所有数列
,写出创新数列为3,4,4,4的所有数列 ;
;
(2)是否存在数列 的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由.
的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由.
(3)是否存在数列 ,使它的创新数列为等差数列?若存在,求出满足所有条件的数列
,使它的创新数列为等差数列?若存在,求出满足所有条件的数列 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市高三模拟考试理科数学 题型:解答题
(本题满分14分,其中第1小题6分,第2小题8分)
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度 (单位:cm)满足关系:
(单位:cm)满足关系: ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求 的值及
的值及 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年方城一高高三年级10月月考数学试卷(理科) 题型:解答题
(本题满分12分)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度 (单位:cm)满足关系:
(单位:cm)满足关系: ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(Ⅰ)求 的值及
的值及 的表达式;
的表达式;
(Ⅱ)隔热层修建多厚对,总费用 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三下学期期中考试理数 题型:解答题
.(本题满分16分)
已知各项均不为零的数列{an}的前n项和为Sn,且满足a1=c,2Sn=anan+1+r.
(1)若r=-6,数列{an}能否成为等差数列?若能,求 满足的条件;若不能,请说明理由.
满足的条件;若不能,请说明理由.
(2)设 ,
, ,
,
若r>c>4,求证:对于一切n∈N*,不等式 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源:广东省2013届高一下学期期末考试数学 题型:解答题
(本题满分14分).
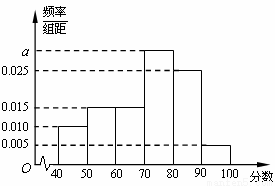
某校从高一年级学生中随机抽取60名学生,将其期中考试的数学成绩(均为整数)分成六段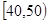 ,
,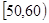 ,…,
,…, 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)求分数在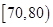 内的频率;
内的频率;
(2)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com