

 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源:不详 题型:解答题
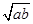 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
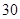 个互异的实数,可以排成
个互异的实数,可以排成 行
行 列的矩形数阵,右图所示的
列的矩形数阵,右图所示的 行
行 列的矩形数阵就是其中之一.将
列的矩形数阵就是其中之一.将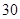 个互异的实数排成
个互异的实数排成 行
行 列的矩形数阵后,把每行中最大的数选出,记为
列的矩形数阵后,把每行中最大的数选出,记为 ,并设其中最小的数为
,并设其中最小的数为 ;把每列中最小的数选出,记为
;把每列中最小的数选出,记为 ,并设其中最大的数为
,并设其中最大的数为 .
.
 和
和 必相等; ②
必相等; ② 和
和 可能相等;
可能相等; 可能大于
可能大于 ; ④
; ④ 可能大于
可能大于 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.甲 | B.乙 | C.丙 | D.丁 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.a3<b3 | B.a3<b3或a3=b3 |
| C.a3<b3且a3=b3 | D.a3>b3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com