
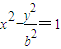 的左、右焦点,A是双曲线上在第一象限内的点,若|AF2|=2且∠F1AF2=45°.廷长AF2交双曲线右支于点B,则△F1AB及的面积等于 .
的左、右焦点,A是双曲线上在第一象限内的点,若|AF2|=2且∠F1AF2=45°.廷长AF2交双曲线右支于点B,则△F1AB及的面积等于 .  ,从而得到
,从而得到 .设A(x1,y1),B(x2,y2).由直线AB方程与双曲线方程联解,算出|y2|=(
.设A(x1,y1),B(x2,y2).由直线AB方程与双曲线方程联解,算出|y2|=( )y1,得到△BF1F2与△AF1F2的面积之比等于
)y1,得到△BF1F2与△AF1F2的面积之比等于 ,结合△AF1F2的面积为
,结合△AF1F2的面积为 =2
=2 得到△BF1F2的面积等于4-2
得到△BF1F2的面积等于4-2 ,再两个三角形的面积相加,即可得到△F1AB及的面积.
,再两个三角形的面积相加,即可得到△F1AB及的面积.
 =(2c)2=42+22-2×4×2×cos45°,化为
=(2c)2=42+22-2×4×2×cos45°,化为 ,
, ,
, ,化为
,化为 .
. ,
, (舍去).
(舍去). ,
, ),
), 联解,可得
联解,可得
 ,结合y1=
,结合y1= 化简得到|y2|=(
化简得到|y2|=( )y1
)y1 =
= =
=
 =
= =
= =2
=2
 =(
=( )S
)S =4-2
=4-2
 +S
+S =4
=4

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 3 |
| ||||
|
|
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、2
| ||||
D、3
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| y2 | b2 |
查看答案和解析>>
科目:高中数学 来源:温州二模 题型:填空题
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:2009年广东省汕头市高考数学一模试卷(文科)(解析版) 题型:选择题
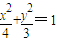 上的点,F1,F2分别是椭圆的左、右焦点,若
上的点,F1,F2分别是椭圆的左、右焦点,若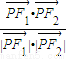 =
= ,则△FIPF2的面积为( )
,则△FIPF2的面积为( )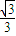
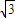

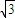
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com