练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】取数游戏：每次游戏中，游戏人按动游泳按钮，就从如图：的三个窗口中各弹出一个数字，其中：最左边窗口可随机弹出数字4或3，中间窗口可随机弹出3或2，最右边窗口可随机弹出2或1.若弹出的三个数字为“顺子”（如：432），则可获奖10元，若有相邻两位数字相同，则可获奖8元，其他情况获奖-2元.甲玩了8次游戏后，乙问甲的获奖情况，甲说：“23元有余，28元不足，3除不尽.”那么甲在这8次游戏中得到“顺子”、“相邻两位数字相同”、“其他情况”的次数依次为（ ）

    A. 0，4，4 B. 2，2，4 C. 2，3，3 D. 1，3，4

    【答案】D

    【解析】填好的三位数可能是： .获10元的有两种情况；获8元的有四种情况；获元的有两种情况．甲获奖的可能有元．但奖金均为偶数.所以只能有24,26元两种可能，又不能被3整除,最后确定奖金为26元,可代答案检验1,3,4符合要求．

    故选： ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】近年来，共享单车已经悄然进入了广大市民的日常生活，并慢慢改变了人们的出行方式.为了更好地服务民众，某共享单车公司在其官方中设置了用户评价反馈系统，以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出条较为详细的评价信息进行统计，车辆状况的优惠活动评价的列联表如下：

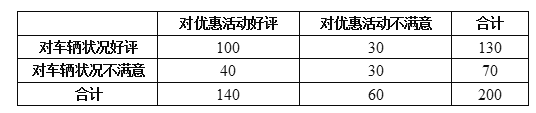
    （1）能否在犯错误的概率不超过的前提下认为优惠活动好评与车辆状况好评之间有关系？

    （2）为了回馈用户，公司通过向用户随机派送骑行券.用户可以将骑行券用于骑行付费，也可以通过转赠给好友.某用户共获得了5张骑行券，其中只有2张是一元券.现该用户从这5张骑行券中随机选取2张转赠给好友，求选取的张中至少有1张是一元券的概率.

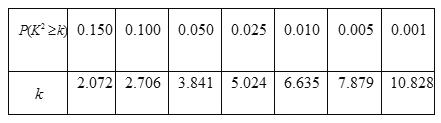
    参考公式：，其中.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

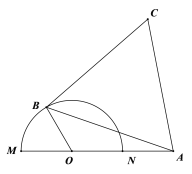
    【题目】如图半圆的直径为4，为直径延长线上一点，且，为半圆周上任一点，以为边作等边（、、按顺时针方向排列）

    （1）若等边边长为，，试写出关于的函数关系；

    （2）问为多少时，四边形的面积最大？这个最大面积为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠BCD=135°，侧面PAB⊥底面ABCD，∠BAP=90°，AB=AC=PA=2，E、F分别为BC、AD的中点，点M在线段PD上．

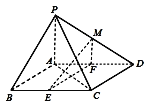
    (1)求证：EF⊥平面PAC；

    (2)如果直线ME与平面PBC所成的角和直线ME与平

    面ABCD所成的角相等，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象上的一个最低点为，周期为.

    （1）求的解析式；

    （2）将的图象上的所有点的横坐标伸长到原来的2倍（纵坐标不变），然后再将所得的图象沿轴向右平移个单位，得到函数的图象，写出函数的解析式；

    （3）当时，求函数的最大值和最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥中，交于点,且，

    。

    （1）若为中点，求证：∥。

    （2）当三棱锥的体积最大时，求三棱锥的体积，并证明：。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱台中，底面是菱形，，，平面．

    （1）若点是的中点，求证：//平面；

    （2）棱BC上是否存在一点E，使得二面角的余弦值为？若存在，求线段CE的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）求函数的单调区间；

    （2）若对于任意， ，恒有成立，试求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据国家环保部最新修订的《环境空气质量标准》规定：居民区PM2.5的年平均浓度不得超过35微克/立方米，PM2.5的24小时平均浓度不得超过75微克/立方米。某城市环保部分随机抽取的一居民区过去20天PM2.5的24小时平均浓度的监测数据，数据统计如下：

    组别

    PM2.5平均浓度

    频数

    频率

    第一组

    （0,25]

    3

    0.15

    第二组

    （25,50]

    12

    0.6

    第三组

    （50,75]

    3

    0.15

    第四组

    （75,100]

    2

    0.1

    （Ⅰ）从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中，随机抽取2天，求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率；

    （II）求样本平均数，并根据样本估计总计的思想，从PM2.5的年平均浓度考虑，判断该居民区的环境是否需要改进?并说明理由.

    查看答案和解析>>

    同步练习册答案