练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
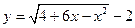
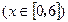    将函数的图像绕坐标原点逆时针方向旋转角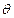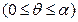，得到曲线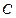.若对于每一个旋转角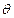，曲线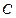都是一个函数的图像，则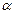的最大值为__________
    由可得，所以函数表示的图象是在时，以为圆心、半径为的一段圆弧，设过原点且与曲线相切的直线方程为，当时，设此时直线的倾斜角为，则.当切线方程和轴重合时，曲线上的点满足函数的定义，即是一个函数图象，再逆时针旋转，曲线不再是一个函数的图象，所以，旋转角为，则，即
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    对任意x∈R，若关于x的不等式ax2 – |x + 1| + 2a≥0恒成立，则实数a的取值范围是．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （12分）已知函数。当时，函数的取值范围恰为。
    （1）求函数的解析式；（2）若向量，解关于的不等式。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

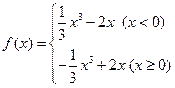    已知函数,下列四个命题中：①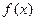是奇函数; ②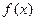是偶函数; ③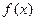的最大值是2;④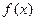在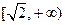上是减函数.其中说法正确的命题序号是      . (写出所有正确命题的序号).

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

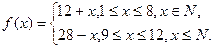    （本小题满分12分）某地一水库年初有水量a(a≥10000)，其中含污染物的量为p0（设水与污染物混合均匀），已知该地降水量与月份的关系为而每月流入水库的污水量与蒸发的水量都是r，且此污水中含污染物的量为p(p<r)，设当年水库中的水不作它用.
    （Ⅰ）求第x月水库中水的含污比g(x)的表达式（含污比=）；
    （Ⅱ）当p0­=0时，求水质量差的月份及此月的含污比.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    (本小题满分16分)
    按照某学者的理论，假设一个人生产某产品单件成本为元，如果他卖出该产品的单价为元，则他的满意度为；如果他买进该产品的单价为元，则他的满意度为.如果一个人对两种交易(卖出或买进)的满意度分别为和，则他对这两种交易的综合满意度为.
    现假设甲生产A、B两种产品的单件成本分别为12元和5元，乙生产A、B两种产品的单件成本分别为3元和20元，设产品A、B的单价分别为元和元，甲买进A与卖出B的综合满意度为，乙卖出A与买进B的综合满意度为
    (1)求和关于、的表达式；当时，求证：=；
    (2)设，当、分别为多少时，甲、乙两人的综合满意度均最大？最大的综合满意度为多少？(3)记(2)中最大的综合满意度为，试问能否适当选取、的值，使得和同时成立，但等号不同时成立？试说明理由。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

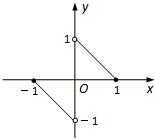
    函数y=f（x）的图象是两条直线的一部分（如图所示），其定义域为[-1，0）∪（0，1]，则不等式f（x）-f（-x）＞-1的解集为______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知直角坐标平面上任意两点，定义
    ．
    当平面上动点到定点的距离满足时，则的取值范围是    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    定义在R上的函数， （  ）
    A．-3B．3C．6D．-6

    查看答案和解析>>

    同步练习册答案