
分析 (Ⅰ)利用三角恒等变换化简函数f(x)的解析式,再利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
(Ⅱ)利用正弦函数的图象的对称性,求得φ的值.
(Ⅲ)设当x=θ时,利用辅助角公式,求得g(x)=f(x)+sinx取得最大值时,cosθ的值.
解答 解:(Ⅰ)∵函数f(x)=2sin$\frac{x}{2}$cos$\frac{x}{2}$-2$\sqrt{3}$sin2$\frac{x}{2}$+$\sqrt{3}$=sinx+$\sqrt{3}$cosx=2sin(x+$\frac{π}{3}$),
故把y=sinx的图象向左平移$\frac{π}{3}$个单位,可得y=sin(x+$\frac{π}{3}$)的图象,
再把各点的纵坐标变为原来的2倍,可得f(x)=2sin(x+$\frac{π}{3}$)的图象.
(Ⅱ)若y=f(x+φ)=2sin(x+φ+$\frac{π}{3}$)的一个对称中心为($\frac{π}{3}$,0),
则$\frac{π}{3}$+φ+$\frac{π}{3}$=kπ,k∈Z,∴φ=$\frac{π}{3}$.
(Ⅲ)设当x=θ时,函数g(x)=f(x)+sinx=2sin(θ+$\frac{π}{3}$)+sinθ=2sinθ+$\sqrt{3}$cosθ=$\sqrt{7}$($\frac{2}{\sqrt{7}}$sinθ+$\frac{\sqrt{3}}{\sqrt{7}}$cosθ)
=$\sqrt{7}$sin(θ+arcsin$\frac{\sqrt{3}}{\sqrt{7}}$)取得最大为$\sqrt{7}$,此时,sinθ=$\frac{2}{\sqrt{7}}$,cosθ=$\frac{\sqrt{3}}{\sqrt{7}}$.
点评 本题主要考查三角恒等变换,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,辅助角公式的应用,属于中档题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源:2015-2016学年河南省商丘市高一理下学期期末考数学试卷(解析版) 题型:解答题
如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min 后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1 260 m,经测量,cos A=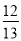 ,cos C=
,cos C=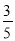 .
.
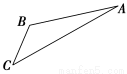
(Ⅰ)求索道AB的长;
(Ⅱ)问:乙出发多少分钟后,乙在缆车上与甲的距离最短?
(Ⅲ)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AD}$•($\overrightarrow{AB}$-$\overrightarrow{AC}$)=0 | B. | |$\overrightarrow{AB}$+$\overrightarrow{AC}$|≥2|$\overrightarrow{AD}$| | C. | $\overrightarrow{AC}$•$\overrightarrow{AD}$=|$\overrightarrow{AC}$|2 | D. | $\overrightarrow{AC}$•$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$=|$\overrightarrow{AB}$|sinB |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com