
【题目】函数![]() 满足:
满足:
①![]() ;②在区间
;②在区间![]() 内有最大值无最小值;
内有最大值无最小值;
③在区间![]() 内有最小值无最大值;④经过
内有最小值无最大值;④经过![]()
(1)求![]() 的解析式;
的解析式;
(2)若![]() ,求
,求![]() 值;
值;
(3)不等式![]() 的解集不为空集,求实数
的解集不为空集,求实数![]() 的范围.
的范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据条件①②③可判断出![]() 和
和![]() 为
为![]() 的两条相邻的对称轴,由此可知周期
的两条相邻的对称轴,由此可知周期![]() ,进而得到
,进而得到![]() ;根据条件①②知
;根据条件①②知![]() ;当
;当![]() 时,
时,![]() 的取值不合题意,可知
的取值不合题意,可知![]() ,此时可求出
,此时可求出![]() ;代入点
;代入点![]() 可求得
可求得![]() ,从而得到函数解析式;(2)通过已知等式可求得
,从而得到函数解析式;(2)通过已知等式可求得![]() ;利用诱导公式变形可知
;利用诱导公式变形可知![]() ,根据同角三角函数平方关系求得结果;(3)设
,根据同角三角函数平方关系求得结果;(3)设![]() ,则
,则![]() ,将不等式解集不为空集等价于
,将不等式解集不为空集等价于![]() ,根据二次函数图象可求得最大值,从而得到不等式,解不等式求得结果.
,根据二次函数图象可求得最大值,从而得到不等式,解不等式求得结果.
(1)由![]() 和条件②知:
和条件②知:![]() 为
为![]() 的一条对称轴,且
的一条对称轴,且![]() 在
在![]() 处取得最大值
处取得最大值
由![]() 和条件③知:
和条件③知:![]() 为
为![]() 的一条对称轴,且
的一条对称轴,且![]() 在
在![]() 处取得最小值
处取得最小值
综合条件①②③可知![]() 和
和![]() 为相邻对称轴
为相邻对称轴
![]() ,解得:
,解得:![]()
![]()
若![]() ,则
,则![]() ,即
,即![]()
不符合![]()
![]()
![]() ,即
,即![]()
又![]()
![]()
由条件④知:![]() ,解得:
,解得:![]()
![]()
(2)由(1)知,![]()
![]()
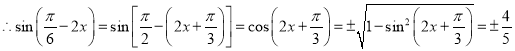
(3)![]()
![]()
令![]() ,则不等式可表示为:
,则不等式可表示为:![]()
又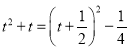
![]()
不等式有解,则![]() ,解得:
,解得:![]()
即不等式![]() 的解集不为空集时,
的解集不为空集时,![]()


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】在十九大“建设美丽中国”的号召下,某省级生态农业示范县大力实施绿色生产方案,对某种农产品的生产方式分别进行了甲、乙两种方案的改良。为了检查甲、乙两种方案的改良效果,随机在这两种方案中各任意抽取了40件产品作为样本逐件称出它们的重量(单位:克),重量值落在![]() 之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
产品重量 | 甲方案频数 | 乙方案频数 |
| 6 | 2 |
| 8 | 12 |
| 14 | 18 |
| 8 | 6 |
| 4 | 2 |
(1)根据上表数据求甲(同组中的重量值用组中点数值代替)方案样本中40件产品的平均数和中位数
(2)由以上统计数据完成下面![]() 列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
甲方案 | 乙方案 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
参考公式:![]() ,其中
,其中![]() .
.
临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.814 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构用“10分制”调查了各阶层人士对某次国际马拉松赛事的满意度,现从调查人群中随机抽取16名,如图茎叶图记录了他们的满意度分数![]() 以小数点前的一位数字为茎,小数点后的一位数字为叶
以小数点前的一位数字为茎,小数点后的一位数字为叶![]() :
:

(1)指出这组数据的众数和中位数;
(2)若满意度不低于![]() 分,则称该被调查者的满意度为“极满意”,求从这16人中随机选取3人,至少有2人满意度是“极满意”的概率;
分,则称该被调查者的满意度为“极满意”,求从这16人中随机选取3人,至少有2人满意度是“极满意”的概率;
(3)以这16人的样本数据来估计整个被调查群体的总体数据,若从该被调查群体![]() 人数很多
人数很多![]() 任选3人,记
任选3人,记![]() 表示抽到“极满意”的人数,求
表示抽到“极满意”的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆![]() >
>![]() >0
>0![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“准圆”.若椭圆
的“准圆”.若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上的一个端点到
,其短轴上的一个端点到![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点![]() 是椭圆
是椭圆![]() 的“准圆”上的一个动点,过点
的“准圆”上的一个动点,过点![]() 作直线
作直线![]() ,使得
,使得![]() 与椭圆
与椭圆![]() 都只有一个交点.求证:
都只有一个交点.求证:![]() ⊥
⊥![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域和值域均为![]() (常数
(常数![]() )的函数
)的函数![]() 和y=g(x)的图像如图所示,给出下列四个命题:
和y=g(x)的图像如图所示,给出下列四个命题:
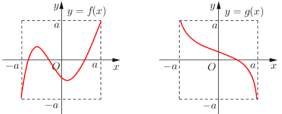
(1)方程![]() 有且仅有三个解;
有且仅有三个解;
(2)方程![]() 有且仅有三个解;
有且仅有三个解;
(3)方程![]() 有且仅有九个解;
有且仅有九个解;
(4)方程![]() 有且仅有一个解;
有且仅有一个解;
那么,其中正确命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等腰梯形MNCD中,MD∥NC,MN=![]() MD=2,∠CDM=60°,E为线段MD上一点,且ME=3,以EC为折痕将四边形MNCE折起,使MN到达AB的位置,且AE⊥DC
MD=2,∠CDM=60°,E为线段MD上一点,且ME=3,以EC为折痕将四边形MNCE折起,使MN到达AB的位置,且AE⊥DC

(1)求证:DE⊥平面ABCE;
(2)求点A到平面DBE的距离
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() ,椭圆
,椭圆![]() 的中心在原点,
的中心在原点,![]() 为其右焦点,点
为其右焦点,点![]() 为曲线
为曲线![]() 和
和![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为抛物线
为抛物线![]() 上的两个动点,且使得线段
上的两个动点,且使得线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,
上,
![]() 为定点,求
为定点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com