练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数，.

    （1）当为何值时，轴为曲线的切线；

    （2）用表示、中的最大值，设函数，当时，讨论零点的个数.

    【答案】（1）；（2）见解析.

    【解析】

    （1）设切点坐标为，然后根据可解得实数的值；

    （2）令，，然后对实数进行分类讨论，结合和的符号来确定函数的零点个数.

    （1），，

    设曲线与轴相切于点，则，

    即，解得.

    所以，当时，轴为曲线的切线；

    （2）令，，

    则，，由，得.

    当时，，此时，函数为增函数；当时，，此时，函数为减函数.

    ，.

    ①当，即当时，函数有一个零点；

    ②当，即当时，函数有两个零点；

    ③当，即当时，函数有三个零点；

    ④当，即当时，函数有两个零点；

    ⑤当，即当时，函数只有一个零点.

    综上所述，当或时，函数只有一个零点；

    当或时，函数有两个零点；

    当时，函数有三个零点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中为常数.

    （1）讨论函数的单调性；

    （2）当（为自然对数的底数），时，若方程有两个不等实数根，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f(x)＝|2x＋4|＋|x－3|.

    (1)解关于x的不等式f(x)<8；

    (2)对于正实数a，b，函数g(x)＝f(x)－3a－4b只有一个零点，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，动直线与椭圆交于点，与轴交于点.为坐标原点，是中点.

    （1）若，求的面积；

    （2）若试探究是否存在常数，使得是定值？若存在，求的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面平面ABCD，，，底面ABCD是边长为2的菱形，点E，F分别为棱DC，BC的中点，点G是棱SC靠近点C的四等分点.

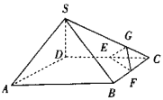
    求证：（1）直线平面EFG；

    （2）直线平面SDB.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了了解游客的情况，以便制定相应的策略，在某月中随机抽取甲、乙两个景点各10天的游客数，画出茎叶图如图：

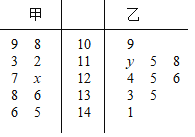
    （1）若景点甲中的数据的中位数是125，景点乙中的数据的平均数是124，求x，y的值；

    （2）若将图中景点甲中的数据作为该景点较长一段时期内的样本数据.今从这段时期中任取4天，记其中游客数超过120人的天数为，求概率；

    （3）现从如图所示的共20天的数据中任取2天的数据（甲、乙两景点中各取1天），记其中游客数不低于115且不高于125人的天数为，求的分布列和期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    设函数

    （Ⅰ）若是函数的极值点，1和是的两个不同零点，且

    且，求的值；

    （Ⅱ）若对任意, 都存在（ 为自然对数的底数），使得

    成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，底面为直角梯形，∥，，，，为的中点.

    （Ⅰ）证明：∥平面；

    （Ⅱ）若，求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数(mR)的导函数为．

    （1）若函数存在极值，求m的取值范围；

    （2）设函数（其中e为自然对数的底数），对任意mR，若关于x的不等式在(0，)上恒成立，求正整数k的取值集合．

    查看答案和解析>>

    同步练习册答案