
【题目】已知![]() .
.
(1)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(2)证明:当![]() 时,
时,![]() .
.
【答案】(1) ![]() (2)证明见解析
(2)证明见解析
【解析】
(1)求导![]() ,
,![]() ,讨论
,讨论![]() 与1 的大小确定
与1 的大小确定![]() 的正负,进而确定
的正负,进而确定![]() 的最值即可证明
的最值即可证明
(2)由(1)取![]() ,得
,得![]() ,要证
,要证![]() ,只需证
,只需证![]() ,构造函数
,构造函数![]() ,证明
,证明![]() 即可证明
即可证明
(1)法一:由题意![]() ,
,![]()
① 若![]() ,即
,即![]() 时,
时,![]() ,则
,则![]() 在
在![]() 单调递增,
单调递增,
则![]() ,则
,则![]() 在
在![]() 单调递增,故
单调递增,故![]() ,满足题意;
,满足题意;
② 若![]() ,即
,即![]() 时,存在
时,存在![]() ,使得
,使得![]() ,且当
,且当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,则
,则![]() 在
在![]() 单调递减,此时
单调递减,此时![]() ,舍去;
,舍去;
③ 若![]() ,即
,即![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,则
,则![]() 在
在![]() 单调递减,
单调递减, ![]() ,舍去;
,舍去;
故![]() .
.
法二:由题知![]() ,且
,且![]() ,
,![]() ,
,![]()
要使得![]() 在
在![]() 上恒成立,则必须满足
上恒成立,则必须满足![]() ,即
,即![]() ,
,![]() .
.
① 若![]() 时,
时,![]() ,则
,则![]() 在
在![]() 单调递增,则
单调递增,则![]() ,
,
则![]() 在
在![]() 单调递增,故
单调递增,故![]() ,满足题意;
,满足题意;
② 若![]() 时,存在
时,存在![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,则
,则![]() 在
在![]() 单调递减,此时
单调递减,此时![]() ,舍去;
,舍去;
故![]() .
.
(2)证明:由(1)知,当![]() 时,
时,![]() .取
.取![]() ,
,
则![]()
由(1)![]() ,则
,则![]() ,故
,故![]() ,
,
要证![]() ,只需证
,只需证![]() .
.
令![]() ,则
,则![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增,有
上单调递增,有![]() ,
,
故![]() 在
在![]() 单调递增,故
单调递增,故![]() ,
,
故![]() ,即有
,即有![]() ,得证
,得证


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,若关于
时,若关于![]() 的方程
的方程![]() 有唯一实数解,试求实数
有唯一实数解,试求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且不等式
,且不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有40名高中生参加足球特长生初选,第一轮测身高和体重,第二轮足球基础知识问答,测试员把成绩(单位:分)分组如下:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到频率分布直方图如图所示.
,得到频率分布直方图如图所示.
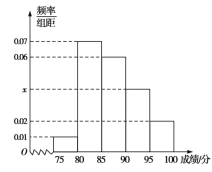
(1)根据频率分布直方图估计成绩的平均值(同一组中的数据用该组区间的中点值作代表);
(2)用分层抽样的方法从成绩在第3,4,5组的高中生中抽取6名组成一个小组,若再从这6人中随机选出2人担任小组负责人,求这2人来自第3,4组各1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x-![]() (a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(1)若对[1,+![]() )内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
)内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
(2)当a=l时,求最大的正整数k,使得对[e,3](e=2.71828是自然对数的底数)内的任意k个实数x1,x2,,xk都有![]() 成立;
成立;
(3)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的侧面
的侧面![]() 是平行四边形,
是平行四边形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 分别是
分别是![]() 的中点.
的中点.

(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部门共有4名员工, 某次活动期间, 周六、 周日的上午、 下午各需要安排一名员工值班,若规定同一天的两个值班岗位不能安排给同一名员工, 则该活动值班岗位的不同安排方式共有( )
A.120种B.132种C.144种D.156种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com