
【题目】已知函数![]() ,
,![]() (
(![]() ).
).
(1)若![]() ,求
,求![]() 在
在![]() 上的最小值;
上的最小值;
(2)若![]() 对于任意的实数
对于任意的实数![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值.
上的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)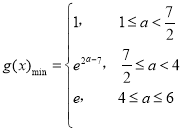 .
.
【解析】
(1)利用基本不等式求解最值;
(2)转化为![]() 对于任意的实数x恒成立,求参数的取值范围;
对于任意的实数x恒成立,求参数的取值范围;
(3)函数去绝对值,等价转化为比较![]() 与
与![]() 的大小关系,数形结合求解.
的大小关系,数形结合求解.
(1)对于![]() ,
,![]() ,
,
所以![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立,所以
时等号成立,所以![]() .
.
(2)![]() 对于任意的实数x恒成立,即
对于任意的实数x恒成立,即![]() 对于任意的实数x恒成立,亦即
对于任意的实数x恒成立,亦即![]() 对于任意的实数x恒成立,
对于任意的实数x恒成立,
所以![]() ,即
,即![]() 对于任意的实数x恒成立.
对于任意的实数x恒成立.
又![]() 对于任意的实数x恒成立,
对于任意的实数x恒成立,
故只需![]() ,解得
,解得![]() ,所以
,所以![]() 的取值范围为
的取值范围为![]() .
.
(3)![]()
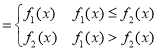 ,
,
因为![]() 与
与![]() 的底数都同为e,外函数都单调递增,
的底数都同为e,外函数都单调递增,
所以,比较![]() 与
与![]() 的大小关系,只须比较
的大小关系,只须比较![]() 与
与![]() 的大小关系.
的大小关系.
令![]() ,
,![]() ,
,
 ,其中
,其中![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() .
.
令![]() ,得
,得![]() ,由题意可得如下图象:
,由题意可得如下图象:
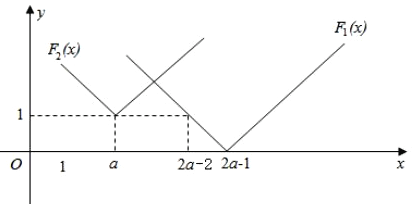
(i)当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ;
;
(ii)当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ;
;
(iii)当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ;
;
综上所述,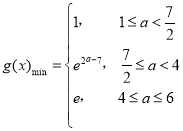 .
.


科目:高中数学 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家大约在公元222年赵爽为《周碑算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的)类比“赵爽弦图”,赵爽弦图可类似地构造如图所示的图形,它是由个3全等的等边三角形与中间的一个小等边三角形组成的一个大等边三角形,设DF2AF,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市约有20万住户,为了节约能源,拟出台“阶梯电价”制度,即制定住户月用电量的临界值![]() ,若某住户某月用电量不超过
,若某住户某月用电量不超过![]() 度,则按平价(即原价)0.5(单位:元/度)计费;若某月用电量超过
度,则按平价(即原价)0.5(单位:元/度)计费;若某月用电量超过![]() 度,则超出部分按议价
度,则超出部分按议价![]() (单位:元/度)计费,未超出部分按平价计费.为确定
(单位:元/度)计费,未超出部分按平价计费.为确定![]() 的值,随机调查了该市100户的月用电量,统计分析后得到如图所示的频率分布直方图.根据频率分布直方图解答以下问题(同一组数据用该区间的中点值作代表).
的值,随机调查了该市100户的月用电量,统计分析后得到如图所示的频率分布直方图.根据频率分布直方图解答以下问题(同一组数据用该区间的中点值作代表).
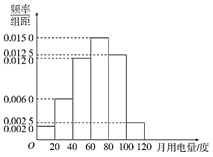
(1)若该市计划让全市![]() 的住户在“阶梯电价”出台前后缴纳的电费不变,求临界值
的住户在“阶梯电价”出台前后缴纳的电费不变,求临界值![]() ;
;
(2)在(1)的条件下,假定出台“阶梯电价”之后,月用电量未达![]() 度的住户用电量保持不变;月用电量超过
度的住户用电量保持不变;月用电量超过![]() 度的住户节省“超出部分”的
度的住户节省“超出部分”的![]() ,试估计全市每月节约的电量;
,试估计全市每月节约的电量;
(3)在(1)(2)条件下,若出台“阶梯电价”前后全市缴纳电费总额不变,求议价![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,
中,![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() .
.
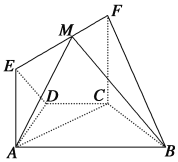
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 、
、![]() ,给出下列四个结论:
,给出下列四个结论:
①![]() ;
;
②若![]() 为直角三角形,则
为直角三角形,则![]() ;
;
③![]() 外接圆的方程为
外接圆的方程为![]() ;
;
④直线![]() 的方程为
的方程为![]() .
.
其中所有正确结论的序号为( )
A.②④B.③④C.②③D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂采用甲、乙两种不同生产方式生产某零件,现对两种生产方式所生产的这种零件的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 100的为一等品;指标在区间
100的为一等品;指标在区间![]() 的为二等品
的为二等品![]() 现分别从甲、乙两种不同生产方式所生产的零件中,各自随机抽取100件作为样本进行检测,测试指标结果的频率分布直方图如图所示:
现分别从甲、乙两种不同生产方式所生产的零件中,各自随机抽取100件作为样本进行检测,测试指标结果的频率分布直方图如图所示:
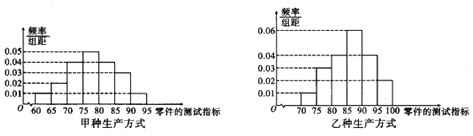
![]() 若在甲种生产方式生产的这100件零件中按等级,利用分层抽样的方法抽取10件,再从这10件零件中随机抽取3件,求至少有1件一等品的概率;
若在甲种生产方式生产的这100件零件中按等级,利用分层抽样的方法抽取10件,再从这10件零件中随机抽取3件,求至少有1件一等品的概率;
![]() 将频率分布直方图中的频率视作概率,用样本估计总体
将频率分布直方图中的频率视作概率,用样本估计总体![]() 若从该厂采用乙种生产方式所生产的所有这种零件中随机抽取3件,记3件零件中所含一等品的件数为X,求X的分布列及数学期望.
若从该厂采用乙种生产方式所生产的所有这种零件中随机抽取3件,记3件零件中所含一等品的件数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请解答以下问题,要求解决两个问题的方法不同.
(1)如图1,要在一个半径为1米的半圆形铁板中截取一块面积最大的矩形![]() ,如何截取?并求出这个最大矩形的面积.
,如何截取?并求出这个最大矩形的面积.
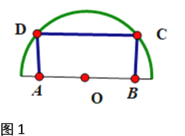
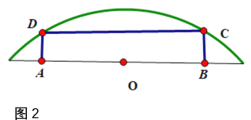
(2)如图2,要在一个长半轴为2米,短半轴为1米的半个椭圆铁板中截取一块面积最大的矩形![]() ,如何截取?并求出这个最大矩形的面积.
,如何截取?并求出这个最大矩形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com