
【题目】请解答以下问题,要求解决两个问题的方法不同.
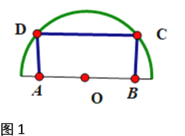
(1)如图1,要在一个半径为1米的半圆形铁板中截取一块面积最大的矩形![]() ,如何截取?并求出这个最大矩形的面积.
,如何截取?并求出这个最大矩形的面积.
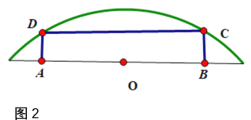
(2)如图2,要在一个长半轴为2米,短半轴为1米的半个椭圆铁板中截取一块面积最大的矩形![]() ,如何截取?并求出这个最大矩形的面积.
,如何截取?并求出这个最大矩形的面积.
【答案】(1)![]() ,面积最大为1(2)
,面积最大为1(2)![]() ,
,![]() ,面积最大值为2
,面积最大值为2
【解析】
(1)通过设出∠BOC=α,进而用α表示出OB,BC;最后表示出S利用三角函数即可求解;
(2)通过设出点C的坐标(m,n),进而表示出OB=m,BC=n,S=2mn;再利用点C为椭圆上的点,即满足其方程利用基本不等式求解即可;
(1)设∠BOC=α,(![]() );
);
∴OB=cosα,BC=sinα;
∵S=2OBBC,
∴S═2sinαcosα=sin2α;
∴当![]() 时,即OA
时,即OA![]() 时,矩形面积最大为1;
时,矩形面积最大为1;
(2)依题意可得:椭圆方程为:![]() ;
;
设:点C坐标为(m,n)即:OB=m,BC=n;
∴S=2OBBC=2mn;
∵点C为椭圆上的点;
∴![]() ;
;
∵![]() ;
;
∴mn≤1,当且仅当![]() 时取等号;
时取等号;
∴S≤2;即矩形面积最大为2;当OB![]() ,即
,即![]() 时取等号;
时取等号;


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是( ).
①在![]() 中,若
中,若![]() ,则
,则![]() 是等腰三角形;
是等腰三角形;
②在![]() 中,若
中,若 ![]() ,则
,则![]()
③两个向量![]() ,
,![]() 共线的充要条件是存在实数
共线的充要条件是存在实数![]() ,使
,使![]()
④等差数列的前![]() 项和公式是常数项为0的二次函数.
项和公式是常数项为0的二次函数.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成.为保证安全,要求行使车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5米.若行车道总宽度AB为6米,则车辆通过隧道的限制高度是______米(精确到0.1米)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对的边分别为a,b,c,已知asinB=bsin2A.
(1)求角A;
(2)若a=5,△ABC的面积为![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部门共有4名员工, 某次活动期间, 周六、 周日的上午、 下午各需要安排一名员工值班,若规定同一天的两个值班岗位不能安排给同一名员工, 则该活动值班岗位的不同安排方式共有( )
A.120种B.132种C.144种D.156种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图判断闰年的流程图,判断公元1900年、公元2000年、公元2018年、公元2020年这四年中闰年的个数为(nMODm为n除以m的余数)( )
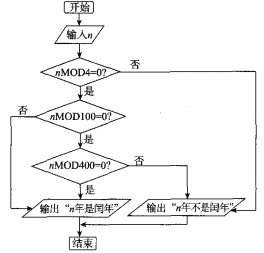
A.1个B.2个
C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的函数,满足
上的函数,满足 .
.
(1)证明:2是函数![]() 的周期;
的周期;
(2)当![]() 时,
时,![]() ,求
,求![]() 在
在![]() 时的解析式,并写出
时的解析式,并写出![]() 在
在![]() (
(![]() )时的解析式;
)时的解析式;
(3)对于(2)中的函数![]() ,若关于x的方程
,若关于x的方程![]() 恰好有20个解,求实数a的取值范围.
恰好有20个解,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com