
【题目】某公司培训员工某项技能,培训有如下两种方式,方式一:周一到周五每天培训1小时,周日测试;方式二:周六一天培训4小时,周日测试.公司有多个班组,每个班组60人,现任选两组(记为甲组、乙组)先培训,甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如下表,其中第一、二周达标的员工评为优秀.
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
(1)在甲组内任选两人,求恰有一人优秀的概率;
(2)每个员工技能测试是否达标相互独立,以频率作为概率.
(i)设公司员工在方式一、二下的受训时间分别为![]() 、
、![]() ,求
,求![]() 、
、![]() 的分布列,若选平均受训时间少的,则公司应选哪种培训方式?
的分布列,若选平均受训时间少的,则公司应选哪种培训方式?
(ii)按(i)中所选方式从公司任选两人,求恰有一人优秀的概率.
【答案】(1)![]() (2)(i)见解析(ii)
(2)(i)见解析(ii)![]()
【解析】
(1)甲组![]() 人中有
人中有![]() 人优秀,利用超几何分布概率计算公式,计算得“甲组内任选两人,求恰有一人优秀的概率”.(2)
人优秀,利用超几何分布概率计算公式,计算得“甲组内任选两人,求恰有一人优秀的概率”.(2)![]() 可能取值有
可能取值有![]() ,根据题目所给数据计算出每种取值对应的频率也即概率,由此得到分布列并其算出期望值.
,根据题目所给数据计算出每种取值对应的频率也即概率,由此得到分布列并其算出期望值.![]() 的所有可能取值为
的所有可能取值为![]() ,根据题目所给数据计算出每种取值对应的频率也即概率,由此得到分布列并其算出期望值.根据两个期望值较小的即为选择.(3)先计算出从公司任选一人,优秀率为
,根据题目所给数据计算出每种取值对应的频率也即概率,由此得到分布列并其算出期望值.根据两个期望值较小的即为选择.(3)先计算出从公司任选一人,优秀率为![]() ,再按照二项分布的概率计算公式计算得“从公司任选两人,求恰有一人优秀的概率”
,再按照二项分布的概率计算公式计算得“从公司任选两人,求恰有一人优秀的概率”
解:(1)甲组60人中有45人优秀,任选两人,
恰有一人优秀的概率为![]() ;
;
(2)(i)![]() 的分布列为
的分布列为
| 5 | 10 | 15 | 20 |
P |
|
|
|
|
![]() ,
,
![]() 的分布列为
的分布列为
| 4 | 8 | 12 | 16 |
P |
|
|
|
|
![]() ,
,
∵![]() ,∴公司应选培训方式一;
,∴公司应选培训方式一;
(ii)按培训方式一,从公司任选一人,其优秀的概率为![]() ,
,
则从公司任选两人,恰有一人优秀的概率为![]() .
.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人做游戏,下列游戏不公平的是( )
A.抛掷一枚骰子,向上的点数为奇数则甲获胜,向上的点数为偶数则乙获胜
B.甲、乙两人各写一个数字1或2,如果两人写的数字相同甲获胜,否则乙获胜
C.从一副不含大小王的扑克牌中抽一张,扑克牌是红色的则甲获胜,扑克牌是黑色的则乙获胜
D.同时抛掷两枚硬币,恰有一枚正面向上则甲获胜,两枚都正面向上则乙获胜
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种型号的农机具零配件,为了预测今年7月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的6组数据如下表所示:
(单位:千件)之间的6组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根据1至6月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件3元,那么工厂如何制定7月份的销售单价,才能使该月利润达到最大?(计算结果精确到0.1)
参考公式:回归直线方程![]() ,
,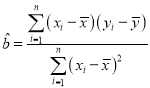
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工企业2018年年底投入100万元,购入一套污水处理设备。该设备每年的运转费用是0.5万元,此外,每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元。设该企业使用该设备![]() 年的年平均污水处理费用为
年的年平均污水处理费用为![]() (单位:万元)
(单位:万元)
(1)用![]() 表示
表示![]() ;
;
(2)当该企业的年平均污水处理费用最低时,企业需重新更换新的污水处理设备。则该企业几年后需要重新更换新的污水处理设备。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,则称这个数为质数.质数的个数是无穷的.设由所有质数组成的无穷递增数列![]() 的前
的前![]() 项和为
项和为![]() ,等差数列1,3,5,7,…中所有不大于
,等差数列1,3,5,7,…中所有不大于![]() 的项的和为
的项的和为![]() .
.
(Ⅰ)求![]() 和
和![]() ;
;
(Ⅱ)判断![]() 和
和![]() 的大小,不用证明;
的大小,不用证明;
(Ⅲ)设![]() ,求证:
,求证:![]() ,
,![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点
的焦点![]() 且斜率为1的直线与抛物线
且斜率为1的直线与抛物线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)点![]() 是抛物线
是抛物线![]() 上异于
上异于![]() 、
、![]() 的任意一点,直线
的任意一点,直线![]() 、
、![]() 与抛物线
与抛物线![]() 的准线分别交于点
的准线分别交于点![]() 、
、![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com