
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若x=2是函数f(x)的极值点,求![]() 在(1,h(1))处的切线方程;
在(1,h(1))处的切线方程;
(2)若对任意的![]() (
(![]() 为自然对数的底数)都有
为自然对数的底数)都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由![]() 是极值点,可知
是极值点,可知![]() ,从而可得
,从而可得![]() 值,再求出
值,再求出![]() ,得
,得![]() ,此为切线斜率,切线方程为
,此为切线斜率,切线方程为![]() ,化简即可;(2)对本小题命题,可求出
,化简即可;(2)对本小题命题,可求出![]() 的最小值
的最小值![]() 和
和![]() 的最大值
的最大值![]() ,命题可转化为
,命题可转化为![]() ,然后可求得
,然后可求得![]() 的范围,
的范围,![]() 最大值由导数的性质易求,由于
最大值由导数的性质易求,由于![]() 中含有参数
中含有参数![]() ,求其最小值时要分类讨论.
,求其最小值时要分类讨论.
试题解析:(1)解:∵![]() , ∵x=2是函数f(x)的极值点,
, ∵x=2是函数f(x)的极值点,
∴![]() , 即
, 即![]() .又a≥1, ∴a=2
.又a≥1, ∴a=2
∴![]() , ∴
, ∴![]() ,
,
∴![]() , 又h(1)=6
, 又h(1)=6
∴所求的切线方程是 y-1=-(x-6),即 y=-x+7.
(2)解:对任意的![]() 都有
都有![]() ≥
≥![]() 成立等价于对任意的
成立等价于对任意的![]() 都有
都有![]() ≥
≥![]()
当![]()
![]() [1,
[1,![]() ]时,
]时,![]() .
.
∴函数![]() 在
在![]() 上是增函数.
上是增函数.
∴![]() .
.
∵![]() ,且
,且![]() ,
,![]() .
.
① 当1≤![]() ≤
≤![]() 时,
时,
若1≤![]() <
<![]() ,则
,则![]() ,
,
若![]() <
<![]() ≤
≤![]() ,则
,则![]() .
.
∴函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
∴![]() .
.
由![]() ≥
≥![]() ,得
,得![]() ≥
≥![]() , 又1≤
, 又1≤![]() ≤
≤![]() ,∴
,∴![]() ≤
≤![]() ≤
≤![]() .
.
②.当![]() 且
且![]()
![]() [1,
[1,![]() ]时,
]时,![]() ,
,
∴函数![]() 在
在![]() 上是减函数.
上是减函数.
∴![]() .由
.由![]() ≥
≥![]() ,得
,得![]() ≥
≥![]() ,
,
又![]() ,∴
,∴![]() .
.
综上所述,![]() 的取值范围为
的取值范围为![]()


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:高中数学 来源: 题型:
【题目】对于定义域为D的函数![]() ,如果存在区间
,如果存在区间![]() ,同时满足:①
,同时满足:①![]() 在
在![]() 内是单调函数;②当定义域是
内是单调函数;②当定义域是![]() 时,
时,![]() 的值域也是
的值域也是![]() .则称
.则称![]() 是该函数的“和谐区间”.
是该函数的“和谐区间”.
(1)证明:![]() 是函数
是函数![]() =
=![]() 的一个“和谐区间”.
的一个“和谐区间”.
(2)求证:函数![]() 不存在“和谐区间”.
不存在“和谐区间”.
(3)已知:函数![]() (
(![]() R,
R,![]() )有“和谐区间”
)有“和谐区间” ![]() ,当
,当![]() 变化时,求出
变化时,求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学的父亲决定今年夏天卖西瓜赚钱,根据去年6月份的数据统计连续五天内每天所卖西瓜的个数与温度之间的关系如下表:
温度 | 32 | 33 | 35 | 37 | 38 |
西瓜个数 | 20 | 22 | 24 | 30 | 34 |
(1)求这五天内所卖西瓜个数的平均值和方差;
(2)求变量![]() 之间的线性回归方程,并预测当温度为
之间的线性回归方程,并预测当温度为![]() 时所卖西瓜的个数.
时所卖西瓜的个数.
附: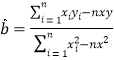 ,
,![]() (精确到
(精确到![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-1:几何证明选讲
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF·EC.

(1)求证:P=EDF;
(2)求证:CE·EB=EF·EP.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax-![]() -5ln x,g(x)=x2-mx+4.
-5ln x,g(x)=x2-mx+4.
(1)若x=2是函数f(x)的极值点,求a的值;
(2)当a=2时,若x1∈(0,1),x2∈[1,2],都有f(x1)≥g(x2)成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
①y与x负相关且![]() =2.347x-6.423;
=2.347x-6.423;
②y与x负相关且![]() =-3.476x+5.648;
=-3.476x+5.648;
③y与x正相关且![]() =5.437x+8.493;
=5.437x+8.493;
④y与x正相关且![]() =-4.326x-4.578.
=-4.326x-4.578.
其中一定不正确的结论的序号是( )
A.①② B.②③ C.③④ D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
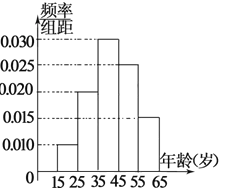
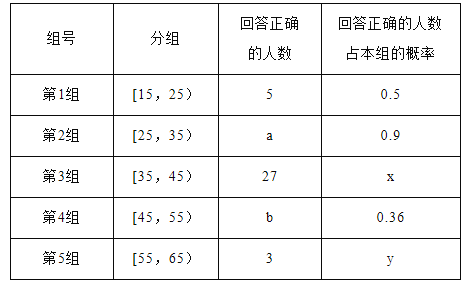
(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取3人颁发幸运奖,求:所抽取的人中第3组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为5的正方形![]() 与矩形
与矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() 分别为
分别为![]() 的中点,
的中点,![]() .
.
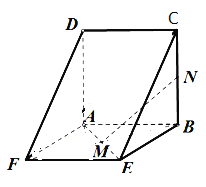
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com