
【题目】选修4-1:几何证明选讲
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF·EC.

(1)求证:P=EDF;
(2)求证:CE·EB=EF·EP.
【答案】证明见解析.
【解析】(1)要证明两角P,EDF相等,注意到![]() ,
, ![]() ,因此只要证C,EDF相等,这两个角正好是可证相似的两个三角形的对应角,这个相似由已知DE2=EF·EC.可证;(2)要证明线段乘积相等,在已知圆中由相交弦定理有CE·EB=ED·EA,再看ED·EA与EF·EP的相等可由相似三角形得到.
,因此只要证C,EDF相等,这两个角正好是可证相似的两个三角形的对应角,这个相似由已知DE2=EF·EC.可证;(2)要证明线段乘积相等,在已知圆中由相交弦定理有CE·EB=ED·EA,再看ED·EA与EF·EP的相等可由相似三角形得到.
试题分析:
试题解析:证明(1)∵DE2=EF·EC,
∴DE : CE=EF: ED.
∵DEF是公共角,
∴ΔDEF∽ΔCED. ∴EDF=C.
∵CD∥AP, ∴C= P.
∴P=EDF.----5分
(2)∵P=EDF, DEF=PEA,
∴ΔDEF∽ΔPEA.∴DE : PE="EF" : EA.即EF·EP=DE·EA.
∵弦AD、BC相交于点E,∴DE·EA=CE·EB.∴CE·EB=EF·EP. 10分


科目:高中数学 来源: 题型:
【题目】某校从参加高二年级期中考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题:

(Ⅰ)求第四小组的频率,补全这个频率分布直方图;并估计该校学生的数学成绩的中位数.(精确到0.1);
(Ⅱ)按分层抽样的方法在数学成绩是[60,70),[70,80)的两组学生中选6人,再在这6人种任取两人,求他们的分数在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装制造商现有300m2的棉布料,900m2的羊毛料,和600 m2的丝绸料。做一条大衣需要1m2的棉布料,5m2的羊毛料,1m2的丝绸料.做一条裤子需要1m2的棉布料,2m2的羊毛料,1m2的丝绸料。
(1)在此基础上生产这两种服装,列出满足生产条件的数学关系式,并在直角坐标系中画出相应的平面区域。
(2)若生产一条大衣的纯收益是120元,生产一条裤子的纯收益是80元,那么应采用哪种生产安排,该服装制造商能获得最大的纯收益;最大收益是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若x=2是函数f(x)的极值点,求![]() 在(1,h(1))处的切线方程;
在(1,h(1))处的切线方程;
(2)若对任意的![]() (
(![]() 为自然对数的底数)都有
为自然对数的底数)都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为4的正方形![]() 与矩形
与矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() 分别为
分别为![]() 的中点,
的中点,![]() .
.
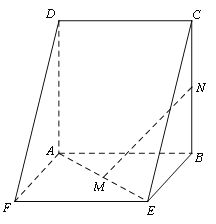
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com