
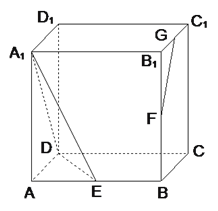
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求二面角![]() 的正切值.
的正切值.
科目:高中数学 来源: 题型:
【题目】对于定义域为D的函数![]() ,如果存在区间
,如果存在区间![]() ,同时满足:①
,同时满足:①![]() 在
在![]() 内是单调函数;②当定义域是
内是单调函数;②当定义域是![]() 时,
时,![]() 的值域也是
的值域也是![]() .则称
.则称![]() 是该函数的“和谐区间”.
是该函数的“和谐区间”.
(1)证明:![]() 是函数
是函数![]() =
=![]() 的一个“和谐区间”.
的一个“和谐区间”.
(2)求证:函数![]() 不存在“和谐区间”.
不存在“和谐区间”.
(3)已知:函数![]() (
(![]() R,
R,![]() )有“和谐区间”
)有“和谐区间” ![]() ,当
,当![]() 变化时,求出
变化时,求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学的父亲决定今年夏天卖西瓜赚钱,根据去年6月份的数据统计连续五天内每天所卖西瓜的个数与温度之间的关系如下表:
温度 | 32 | 33 | 35 | 37 | 38 |
西瓜个数 | 20 | 22 | 24 | 30 | 34 |
(1)求这五天内所卖西瓜个数的平均值和方差;
(2)求变量![]() 之间的线性回归方程,并预测当温度为
之间的线性回归方程,并预测当温度为![]() 时所卖西瓜的个数.
时所卖西瓜的个数.
附: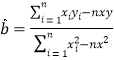 ,
,![]() (精确到
(精确到![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-1:几何证明选讲
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF·EC.

(1)求证:P=EDF;
(2)求证:CE·EB=EF·EP.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
①y与x负相关且![]() =2.347x-6.423;
=2.347x-6.423;
②y与x负相关且![]() =-3.476x+5.648;
=-3.476x+5.648;
③y与x正相关且![]() =5.437x+8.493;
=5.437x+8.493;
④y与x正相关且![]() =-4.326x-4.578.
=-4.326x-4.578.
其中一定不正确的结论的序号是( )
A.①② B.②③ C.③④ D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于![]() ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com