Question

【题目】如图，边长为4的正方形与矩形所在平面互相垂直，分别为的中点，．

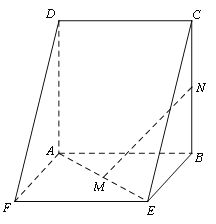
（1）求证：平面；

（2）求证：平面；

（3）在线段上是否存在一点，使得？若存在，求出的长；若不存在，请说明理由．

Answer 1

【答案】（I）详见解析；（Ⅱ）详见解析；（Ⅲ）存在，

【解析】

试题分析：（I）由面面垂直的性质定理可直接证得。（Ⅱ）将转化为的中点，利用中位线证∥，再根据线面平行的判定定理即可证MN∥平面CDFE。（Ⅲ）假设存在点P使AP⊥MN，由（I）易得所以。（Ⅲ）由逆向思维可知只需证得，因为，即可证得AP⊥MN。由相似三角形的相似比即可求得FP。

试题解析：（I）因为为正方形，所以。

因为平面,,，所以.

（Ⅱ）连结

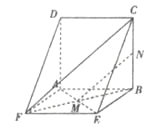
因为是的中点，且为矩形，所以也是的中点。因为是的中点，所以∥，因为,所以MN∥平面CDFE。

（Ⅲ）过点作交线段于点,则点即为所求。因为ABCD为正方形，所以∥。因为，所以，因为,所以。因为，且，所以,因为,所以。因为与相似，所以,因为，所以。