【题目】已知函数
，
.
（1）若函数
在
上不具有单调性，求实数
的取值范围；
（2）若
.
（ⅰ）求实数
的值；
（ⅱ）设
，
，
，当
时，试比较
，
，
的大小．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】甲乙两人进行乒乓球比赛，比赛规则为“三局两胜”即以先赢两局者为胜，根据经验，每局比赛中甲获胜的概率为0.6,则本次比赛甲获胜的概率是（ ）
A. 0.216B. 0.36C. 0.432D. 0.648
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某服装制造商现有300m2的棉布料，900m2的羊毛料，和600 m2的丝绸料。做一条大衣需要1m2的棉布料，5m2的羊毛料，1m2的丝绸料.做一条裤子需要1m2的棉布料，2m2的羊毛料，1m2的丝绸料。
（1）在此基础上生产这两种服装，列出满足生产条件的数学关系式，并在直角坐标系中画出相应的平面区域。
（2）若生产一条大衣的纯收益是120元，生产一条裤子的纯收益是80元，那么应采用哪种生产安排，该服装制造商能获得最大的纯收益；最大收益是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，边长为4的正方形
与矩形
所在平面互相垂直，
分别为
的中点，
．
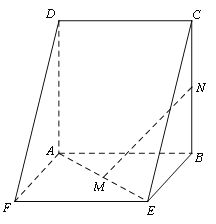
（1）求证：
平面；
（2）求证：
平面
；
（3）在线段
上是否存在一点
，使得
？若存在，求出
的长；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图（如图），其中上面的折线代表可能出现的从高气温，下面的折线代表可能出现的最低气温．
（Ⅰ）指出最高气温与最低气温的相关性；
（Ⅱ）估计在10:00时最高气温和最低气温的差；
（Ⅲ）比较最低气温与最高气温方差的大小（结论不要求证明）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高三年级一次数学考试后，为了解学生的数学学习情况，随机抽取
名学生的数学成绩，制成表所示的频率分布表.
组号 | 分组 | 频数 | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
合计 |
|
| |
（1）求
、
、
的值；
（2）若从第三、四、五组中用分层抽样方法抽取
名学生，并在这
名学生中随机抽取
名学生与张老师面谈，求第三组中至少有
名学生与张老师面谈的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，过点
的直线与抛物线
相交于点
，
两点，设
，
（1）求证：
为定值
（2）是否存在平行于
轴的定直线被以
为直径的圆截得的弦长为定值？如果存在，求出该直线方程和弦长，如果不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
