【题目】已知函数
， 
．
（1）设
，求
的单调区间；
（2）若
在
处取得极大值，求实数
的取值范围．
【答案】（1）单调增区间是
，单调减函数是
；（2）
.
【解析】试题分析：（I）
，先求
导函数
，求导函数零点
，列表分析导函数符号变化规律，确定单调区间（II）由题意得
，且
最大值； 
最大值；而
所以
，也可分类讨论单调性变化规律
试题解析：解：（I）∵
，∴
，
∴
， 
.
当
时，在
上
， 
单调递增；
在
上
， 
单调递减.
∴
的单调增区间是
，单调减区间是
.
（II）∵
在
处取得极大值，∴
.
①当
，即
时，由（I）知
在
上单调递增，在
上单调递减，
∴当
时， 
， 
单调递减，不合题意；
②当
，即
时，由（I）知， 
在
上单调递增，
∴当
时， 
，当
时， 
，
∴
在
上单调递减，在
上单调递增，
∴
在
处取得极小值，不合题意；
③当
，即
时，由（I）知， 
在
上单调递减，
∴当
时， 
，当
时， 
，
∴
在
上单调递增，在
上单调递减，
∴当
时， 
取得极大值，满足条件.
综上，实数
的取值范围是
轻松夺冠全能掌控卷系列答案科目：高中数学 来源： 题型：
【题目】某校从参加高二年级期中考试的学生中抽出60名学生，将其数学成绩（满分100分，均为整数）分成六段[40，50），[50，60）…[90，100]后画出如下部分频率分布直方图．根据图形的信息，回答下列问题：
（Ⅰ）求第四小组的频率，补全这个频率分布直方图；并估计该校学生的数学成绩的中位数．（精确到0.1）；
（Ⅱ）按分层抽样的方法在数学成绩是[60，70），[70，80）的两组学生中选6人，再在这6人种任取两人，求他们的分数在同一组的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，边长为4的正方形
与矩形
所在平面互相垂直，
分别为
的中点，
．
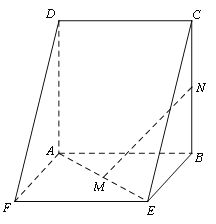
（1）求证：
平面；
（2）求证：
平面
；
（3）在线段
上是否存在一点
，使得
？若存在，求出
的长；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高三年级一次数学考试后，为了解学生的数学学习情况，随机抽取
名学生的数学成绩，制成表所示的频率分布表.
组号 | 分组 | 频数 | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
合计 |
|
| |
（1）求
、
、
的值；
（2）若从第三、四、五组中用分层抽样方法抽取
名学生，并在这
名学生中随机抽取
名学生与张老师面谈，求第三组中至少有
名学生与张老师面谈的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在三棱锥A－BOC中，OA⊥底面BOC，∠OAB＝∠OAC＝30°，AB＝AC＝4，BC＝
，动点D在线段AB上.
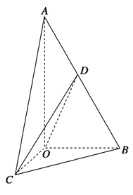
（1）求证：平面COD⊥平面AOB；
（2）当OD⊥AB时，求三棱锥C－OBD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
