
分析 根据函数过点,得到ω=2k-$\frac{1}{2}$,然后结合函数单调性的关系建立不等式条件,进行求解即可.
解答 解:∵函数f(x)=sinωx(其中ω>0)图象过(π,-1)点,
∴f(π)=sinπω=-1,
即πω=2kπ-$\frac{π}{2}$,即ω=2k-$\frac{1}{2}$,
∵在区间(0,$\frac{π}{3}$)上单调递增,
∴$\frac{1}{4}$T=$\frac{1}{4}•\frac{2π}{ω}$≥$\frac{π}{3}$,
即2ω≤3,则0<ω≤$\frac{3}{2}$,
则当k=1时,ω=$\frac{3}{2}$,满足条件.
故答案为:$\frac{3}{2}$.
点评 本题主要考查三角函数单调性的应用,根据函数单调性和周期之间的关系是解决本题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
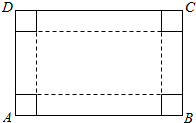 如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).
如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某市乘坐出租车的收费办法如下:
某市乘坐出租车的收费办法如下:| A. | $y=2[x-\frac{1}{2}]+4$ | B. | $y=2[x-\frac{1}{2}]+5$ | C. | $y=2[x+\frac{1}{2}]+4$ | D. | $y=2[x+\frac{1}{2}]+5$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
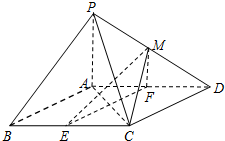 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=6,E,F分别为BC,AD的中点,点M在线段PD上.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=6,E,F分别为BC,AD的中点,点M在线段PD上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | $\frac{\sqrt{15}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{10}}{3}$ | C. | $\sqrt{10}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日销售量 | 1 | 1.5 | 2 |
| 天数 | 10 | 25 | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com