
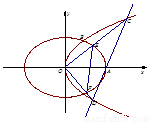
(本小题12分)
如图,抛物线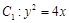 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆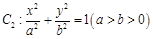 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为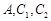 在第一象限的交点为
在第一象限的交点为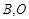 为坐标原点,且
为坐标原点,且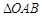 的面积为
的面积为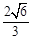
(1)求椭圆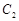 的标准方程;
的标准方程;
(2)过点 作直线
作直线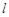 交
交 于
于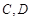 两点,射线
两点,射线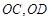 分别交
分别交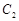 于
于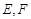 两点.
两点.
(I)求证: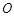 点在以
点在以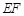 为直径的圆的内部;
为直径的圆的内部;
(II)记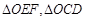 的面积分别为
的面积分别为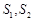 ,问是否存在直线
,问是否存在直线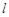 ,使得
,使得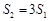 ?请说明理由.
?请说明理由.
科目:高中数学 来源:浏阳一中、田中高三年级2009年下期期末联考试题 数学试题 题型:解答题
(本小题12分)
如图,曲线 是以原点
是以原点 为中心,以
为中心,以 、
、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以
是以 为顶点,以
为顶点,以 为焦点的抛物线的一部分,
为焦点的抛物线的一部分, 是曲线
是曲线 和
和 的交点,且
的交点,且 为钝角,若
为钝角,若 ,
, .
.
(I)求曲线 和
和 所在的椭圆和抛物线的方程;
所在的椭圆和抛物线的方程;
(II)过 作一条与轴不垂直的直线,分别与曲线
作一条与轴不垂直的直线,分别与曲线 、
、 依次交于
依次交于 、
、 、
、 、
、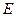 四点(如图),若
四点(如图),若 为
为 的中点,
的中点, 为
为 的中点,问
的中点,问 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011年新疆农七七师高级中学高二下学期第一学段考试理科数学 题型:解答题
(本小题12分)
如图, <
< <
< <…<
<…< )是曲线C
)是曲线C
 :
: 上的n个点,点
上的n个点,点 在x轴的正半轴上,且⊿
在x轴的正半轴上,且⊿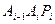 是正三角形(
是正三角形( 是坐标原点)。
是坐标原点)。
(1)写出
(2)求出点 的横坐标
的横坐标 关于n的表达式并用数学归纳法证明
关于n的表达式并用数学归纳法证明
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省协作体高三第三次联考文科数学试卷(解析版) 题型:解答题
(本小题12分)如图,直三棱柱 中,
中,
 ,
, 为
为 中点,若规定主视方向为垂直于平面
中点,若规定主视方向为垂直于平面 的方向,则可求得三棱柱左视图的面积为
的方向,则可求得三棱柱左视图的面积为 ;
;

(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源:2011年四川省高2013届春期重点班第一学月考试数学试题 题型:解答题
(本小题12分)如图,B、A是某海面上位于东西方向相距 海里的两个观测点。现位于B点正北方向、A点北偏东
海里的两个观测点。现位于B点正北方向、A点北偏东 方向的C点有一艘轮船发出求救信号,位于B点北偏西
方向的C点有一艘轮船发出求救信号,位于B点北偏西 、A点北偏西
、A点北偏西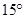 的D点的救援船立即前往营救,其航行速度为
的D点的救援船立即前往营救,其航行速度为 海里/小时.问该救援船到达C点需要多少时间?
海里/小时.问该救援船到达C点需要多少时间?

查看答案和解析>>
科目:高中数学 来源:2011-2012年福建省四地六校高二第二次月考文科数学 题型:解答题
(本小题12分)
如图4:求 的算法的
的算法的
程序框图。⑴标号①处填 。标号②处填 。⑵根据框图用直到型(UNTIL)语句编写程序。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com