分析:(1)设AC1、A1C的交点为O,连结OE.由正三棱柱的性质,证出四边形PA1BB1是平行四边形,得PB1∥A1B.利用三角形中位线定理证出A1B∥OE,得PB1∥OE,利用线面平行的判定定理,即可证出PB1∥面AEC1;
(2)取B1C1中点F,连BF,由异面直线所成角的定义得∠A1BF为PB1与C1E所成的角.在△A1BF中算出各边的长,由余弦定理算出cos∠A1BF的值,即可得到PB1与C1E所成的角的大小;
(3)连A1F,PF,△A1B1C1为正三角形可得A1F⊥B1C1,利用线面垂直的判定与性质和面面垂直判定定理,证出平面PB1C1⊥平面PA1F.作A1H⊥PF于H,可得A1H⊥面PB1C1,即A1H为A1到面PB1C1的距离.Rt△PA1F中,算出斜边上的高A1H的长,结合AP=2A1P可得点A到面PB1C1的距离.
解答:解:(1)∵正三棱柱ABC-A
1B
1C
1中,PA
1BB
1
∴四边形PA
1BB
1是平行四边形,可得PB
1∥A
1B.
设AC
1、A
1C的交点为O,连结OE,可得OE是△A
1BC的中位线,
∴A
1B∥OE,可得PB
1∥OE.
∵PB
1?平面AEC
1,OE?平面AEC
1,∴PB
1∥面AEC
1;
(2)取B
1C
1中点F,连BF,可得BF∥C
1E,
又∵PB
1∥A
1B,∴∠A
1BF为PB
1与C
1E所成的角.
∵在△A
1BF中
A1B=2,BF=,A1F=,
∴由余弦定理,得
cos∠A1BF==,
即得PB
1与C
1E所成的角为
arccos(3)连A
1F、PF,
∵△A
1B
1C
1为正三角形,∴A
1F⊥B
1C
1又∵PA
1⊥面A
1B
1C
1,∴PF⊥B
1G,
∵A
1F、PF是平面PA
1F内的相交直线,∴B
1C
1⊥平面PA
1F,
∵B
1C
1?平面PB
1C
1,∴平面PB
1C
1⊥平面PA
1F
作A
1H⊥PF于H,可得A
1H⊥面PB
1C
1,即A
1H为A
1到面PB
1C
1的距离.
∵Rt△PA
1F中,
PA1=2,A1F=,
∴
PF==,得
A1H==,
又∵AP=2A
1P,∴点A到面PB
1C
1的距离等于
.
点评:本题在正三棱柱中证明线面平行,并求异面直线所成角的大小和点到平面的距离,着重考查了空间垂直与平行位置关系的判断与证明、点到平面面的距离和异面直线所成角的计算等知识,属于中档题.

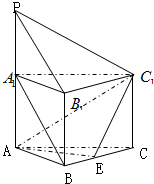 如图,正三棱柱ABC-A1B1C1的每条棱长均为2,PA1⊥平面ABC,PA1=2,E为BC中点.
如图,正三棱柱ABC-A1B1C1的每条棱长均为2,PA1⊥平面ABC,PA1=2,E为BC中点.


 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.