解:(Ⅰ)由已知,根据正弦定理得:2a
2=(2b-c)b+(2c-b)c,…(1分)
即b
2+c
2-a
2=bc,
∴cosA=

=

,…(3分)
∵0<A<π,
∴A=

;…(5分)
(Ⅱ)由(Ⅰ)得:B+C=π-A=

,
设B=

+α,C=

-α,-

<α<

,
∴tanθ=
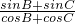
=
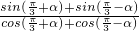
=
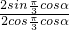
=tan

,
∵0<θ<π,∴θ=

,…(9分)
∴f(x)=2sin(2x+θ)=2sin(2x+

),
∵-

≤x≤-

,-

≤2x+

≤

,
∴当2x+

=-

,即x=-

时,f(x)有最小值-2;
当2x+

=

,即x=-

时,f(x)有最大值1,
则函数f(x)在区间[-

,-

]上的最大值与最小值分别为-2与1.…(12分)
分析:(Ⅰ)利用正弦定理化简已知的等式,再由余弦定理表示出cosA,将得出的等式变形后代入cosA中,求出cosA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数;
(Ⅱ)由A的度数,求出B+C的度数为

,设B=

+α,C=

-α,-

<α<

,代入已知的tanθ的式子中,分子分母分别利用和差化积公式变形后,利用同角三角函数间的基本关系得到tanθ=tan

,由θ的范围得到θ=

,代入函数f(x)解析式中,根据x的范围,得到这个角的范围,利用正弦函数的图象与性质可得出此时函数的最大值及最小值.
点评:此题考查了正弦、余弦定理,和差化积公式,正弦函数的定义域与值域,其中确定出θ的度数是解第二问的关键.

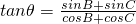 ,且0<θ<π,求函数f(x)=2sin(2x+θ)在区间
,且0<θ<π,求函数f(x)=2sin(2x+θ)在区间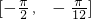 上的最大值与最小值.
上的最大值与最小值. =
= ,…(3分)
,…(3分) ;…(5分)
;…(5分) ,
, +α,C=
+α,C= -α,-
-α,- <α<
<α< ,
,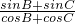 =
=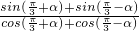 =
=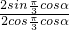 =tan
=tan ,
, ,…(9分)
,…(9分) ),
), ≤x≤-
≤x≤- ,-
,- ≤2x+
≤2x+ ≤
≤ ,
, =-
=- ,即x=-
,即x=- 时,f(x)有最小值-2;
时,f(x)有最小值-2; =
= ,即x=-
,即x=- 时,f(x)有最大值1,
时,f(x)有最大值1, ,-
,- ]上的最大值与最小值分别为-2与1.…(12分)
]上的最大值与最小值分别为-2与1.…(12分) ,设B=
,设B= +α,C=
+α,C= -α,-
-α,- <α<
<α< ,代入已知的tanθ的式子中,分子分母分别利用和差化积公式变形后,利用同角三角函数间的基本关系得到tanθ=tan
,代入已知的tanθ的式子中,分子分母分别利用和差化积公式变形后,利用同角三角函数间的基本关系得到tanθ=tan ,由θ的范围得到θ=
,由θ的范围得到θ= ,代入函数f(x)解析式中,根据x的范围,得到这个角的范围,利用正弦函数的图象与性质可得出此时函数的最大值及最小值.
,代入函数f(x)解析式中,根据x的范围,得到这个角的范围,利用正弦函数的图象与性质可得出此时函数的最大值及最小值.
