
(本题满分12分)三棱锥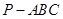 中,
中,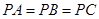 ,
,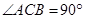 ,
,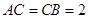 .
.
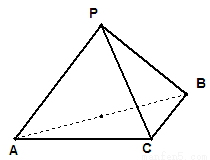
(Ⅰ)求证:平面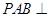 平面
平面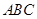 ;
;
(Ⅱ)当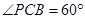 时,求三棱锥
时,求三棱锥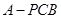 的体积.
的体积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年四川省成都市高三一诊模拟理科数学试卷(解析版) 题型:解答题
(本题满分12分)三棱锥 中,
中, ,
, ,
, .
.

(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)若 ,且异面直线
,且异面直线 与
与 的夹角为
的夹角为 时,求二面角
时,求二面角 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三上学期期末考试理科数学(解析版) 题型:解答题
.(本题满分12分)某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果
如下表所示:
根据上表信息解答以下问题:
(1)从该单位任选两名职工,用 表示这两人休年假次数之和,记“函数
表示这两人休年假次数之和,记“函数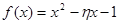 在区间
在区间 ,
,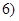 上有且只有一个零点”为事件
上有且只有一个零点”为事件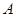 ,求事件
,求事件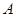 发生的概率
发生的概率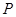 ;
;
(2)从该单位任选两名职工,用 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市高三模拟考试理科数学 题型:解答题
(本题满分12分,其中第1小题6分,第2小题6分)
在直三棱柱 中,
中, ,
, ,且异面直线
,且异面直线 与
与 所成的角等于
所成的角等于 ,设
,设
(1)求 的值;
的值;
(2)求直线 到平面
到平面 的距离。
的距离。

查看答案和解析>>
科目:高中数学 来源:2010年新疆农七师高级中学高二第二学期第二阶段考试数学(理)试题 题型:解答题
(本题满分12分)三人独立破译同一份密码.已知三人各自破译出密码的概率分别为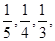 且他们是否破译出密码互不影响.
且他们是否破译出密码互不影响.
(Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com