
| ||
| 2 |
| π |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
| ||
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 5π |
| 6 |
| ||
| 2 |
| π |
| 3 |
| π |
| 2 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| 5π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| π |
| 3 |


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:
| 2 |
| x2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
. |
| x |
. |
| y |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
| 3 |
| π |
| 4 |
A、(-
| ||||||||||||
B、(-
| ||||||||||||
C、(-
| ||||||||||||
D、(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| A、(∁RM)∩N=∅ |
| B、M∪N=R |
| C、M?N |
| D、(∁RM)∪N=R |
查看答案和解析>>
科目:高中数学 来源: 题型:
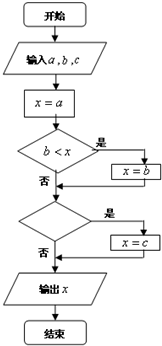 如图所示程序框图中,如果输入三个实数a、b、c,要求输出这三个数中最小的数,那么在空白的判断框中,应该填入下面四个选项中的( )
如图所示程序框图中,如果输入三个实数a、b、c,要求输出这三个数中最小的数,那么在空白的判断框中,应该填入下面四个选项中的( )| A、c<x | B、x<c |
| C、c<b | D、b<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com