
如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.
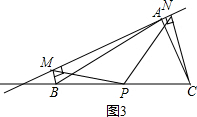
(1)延长MP交CN于点E(如图2).
①求证:△BPM≌△CPE;
②求证:PM=PN;
(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.
(1)结合三角形的边和角来证明全等同时得到线段的对应相等的证明。
(2) PM="PN" 成立,同样是借助于三角形的全等来证明。
(3) “四边形MBCN是矩形,则PM=PN成立”
解析试题分析:(1)证明:①如图2: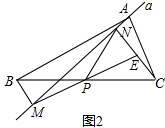
∵BM⊥直线a于点M,CN⊥直线a于点N,
∴∠BMN=∠CNM=90°,
∴BM∥CN,
∴∠MBP=∠ECP,
又∵P为BC边中点,
∴BP=CP,
又∵∠BPM=∠CPE,
∴△BPM≌△CPE, 3分
②∵△BPM≌△CPE,
∴PM=PE∴PM="1" 2 ME,
∴在Rt△MNE中,PN="1" 2 ME, 4分
∴PM=PN.
(2)解:成立,如图3.
证明:延长MP与NC的延长线相交于点E,
∵BM⊥直线a于点M,CN⊥直线a于点N,
∴∠BMN=∠CNM=90°∴∠BMN+∠CNM=180°,
∴BM∥CN∴∠MBP=∠ECP, 6分
又∵P为BC中点,
∴BP=CP,
又∵∠BPM=∠CPE,
∴△BPM≌△CPE,
∴PM=PE,
∴PM="1" 2 ME,
则Rt△MNE中,PN="1" 2 ME,
∴PM=PN. 8分
(3)解:如图4,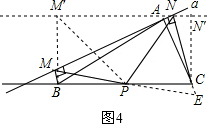
四边形M′BCN′是矩形,
根据矩形的性质和P为BC边中点,得到△M′BP≌△N′CP, 9分
得PM′=PN′成立.即“四边形MBCN是矩形,则PM=PN成立”. 10分
考点:相似三角形
点评:解决该试题的关键是对于相似三角形的性质的熟练运用,属于基础题。


科目:高中数学 来源: 题型:解答题
如图,直线l与⊙O相切于点A,点P为直线l上一点,直线PO交⊙O于点C、B,点D在线段AP上,连结DB,且AD=DB.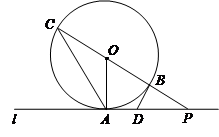
 (1)判断直线DB与⊙O的位置关系,并说明理由;
(1)判断直线DB与⊙O的位置关系,并说明理由;
(2)若PB=BO,⊙O的半径为4cm,求AC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
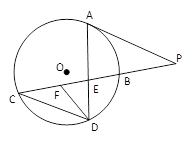
(本小题满分10分)选修4-1:几何证明讲 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F. 
求证:(1) ;
;
(2)AB2=BE•BD-AE•AC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分10分)
如图,已知C、F是以AB为直径的半圆 上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.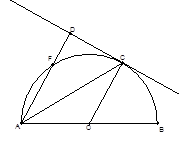
(1)证明:CD为圆O的切线;
(2)若AD=3,AB=4,求AC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)选修4-1:几何证明选讲
如图所示,已知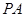 与⊙
与⊙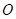 相切,
相切,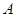 为切点,
为切点,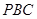 为割线,
为割线,
弦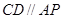 ,
,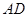 、
、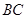 相交于
相交于 点,
点,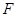 为
为 上一点,且
上一点,且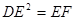 ·
·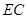 .
.
(1)求证: ;
;
(2)求证: ·
·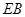 =
= ·
·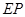 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com