
分析 利用函数单调性的定义即可证明f(x)在(0,+∞)上是增函数.
解答 证明:任取x1,x2∈(0,+∞),且x1<x2,则$\frac{{x}_{2}}{{x}_{1}}$>1,
∵当x>1时,f(x)>1,
∴f($\frac{{x}_{2}}{{x}_{1}}$)>1
∵对x,y∈(0,+∞)恒有f(x•y)=f(x)•f(y),f(x)>0,
∴f(x2)=f($\frac{{x}_{2}}{{x}_{1}}$•x1)=f($\frac{{x}_{2}}{{x}_{1}}$)f(x1)>f(x1),
∴f(x2)>f(x1),
∴f(x)在定义域内是增函数.
点评 本题考查了抽象函数的应用,考查了函数的单调性的判断与证明,考查了学生灵活处理问题和解决问题的能力,属中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:选择题
| A. | 10岁时身高一定是145.83cm | B. | 每长大一岁身高就增高73.93cm | ||
| C. | 每长大一岁身高就增高81.12cm | D. | 10岁时身高在145.83cm左右 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{88}{41}$ | C. | $\frac{28}{17}$ | D. | $\frac{48}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
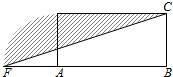 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )| A. | (4π+8)cm2 | B. | (4π+16)cm2 | C. | (3π+8)cm2 | D. | (3π+16)cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com