
【题目】设数列{an}的各项都为正数,其前n项和为Sn , 已知4Sn=an2+2an .
(1)求a1级数列{an}的通项公式;
(2)设数列{bn}前n项和为Tn , 且bn= ![]() ,若λTn<n+(﹣1)n36对n∈N*恒成立,求实数λ的取值范围.
,若λTn<n+(﹣1)n36对n∈N*恒成立,求实数λ的取值范围.
【答案】
(1)解:∵4Sn=an2+2an,
∴4Sn+1=an+12+2an+1,
两式相减得:4an+1=an+12+2an+1﹣(an2+2an),
整理得:(an+1+an)(an+1﹣an)=2(an+1+an),
又∵数列{an}的各项都为正数,
∴an+1﹣an=2,
又∵4a1= ![]() +2a1,
+2a1,
∴a1=2或a1=0(舍),
∴数列{an}的通项公式an=2n
(2)解:bn= ![]()
= ![]()
= ![]()
= ![]() ﹣
﹣ ![]() ,
,
∴Tn=1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =1﹣
=1﹣ ![]() =
= ![]() ,
,
∵λTn<n+(﹣1)n36对n∈N*恒成立,
∴λ< ![]() =n+1+(﹣1)n
=n+1+(﹣1)n ![]() 对n∈N*恒成立,
对n∈N*恒成立,
记f(n)=n+1+(﹣1)n ![]() ,
,
当n为偶数时,f(n)=n+1+ ![]()
=37+n+ ![]()
≥37+2 ![]() =37+26=49,
=37+26=49,
当且仅当n= ![]() 即n=6时取等号;
即n=6时取等号;
当n为奇数时,f(n)=n+1﹣ ![]()
=n﹣ ![]() ﹣35
﹣35
≥1﹣ ![]() ﹣35=﹣70;
﹣35=﹣70;
综上所述,实数λ的取值范围为:(﹣∞,﹣70)
【解析】(1)利用4Sn=an2+2an与4Sn+1=an+12+2an+1作差、整理得an+1﹣an=2,进而计算可得结论;(2)通过裂项、并项相加可知Tn= ![]() ,进而问题转化为求f(n)=n+1+(﹣1)n
,进而问题转化为求f(n)=n+1+(﹣1)n ![]() 的最小值,通过对n分奇数、偶数两种情况讨论即可.
的最小值,通过对n分奇数、偶数两种情况讨论即可.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系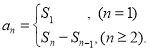 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax﹣(k﹣1)a﹣x(a>0且a≠1)是定义域为R的奇函数.
(1)求k值;
(2)若f(1)= ![]() ,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若把函数y=sin(ωx﹣ ![]() )的图象向左平移
)的图象向左平移 ![]() 个单位,所得到的图象与函数y=cosωx的图象重合,则ω的一个可能取值是( )
个单位,所得到的图象与函数y=cosωx的图象重合,则ω的一个可能取值是( )
A.2
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有极值,且导函数
有极值,且导函数![]() 的极值点是
的极值点是![]() 的零点。(极值点是指函数取极值时对应的自变量的值)
的零点。(极值点是指函数取极值时对应的自变量的值)
求b关于a的函数关系式,并写出定义域;
证明:b>3a;
若![]() ,
,![]() 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于![]() ,求a的取值范围。
,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三角形ABC的边长为2,D、E、F分别在三边AB,BC和CA上,且D为AB的中点,∠EDF=90°,∠BDE=θ(0°<θ<90°). 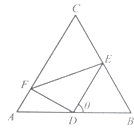
(1)当tan∠DEF= ![]() 时,求θ的大小;
时,求θ的大小;
(2)求△DEF的面积S的最小值及使得S取最小值时θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=sin(ωx+φ)(ω>0,|φ|< ![]() )在同一个周期内,当x=
)在同一个周期内,当x= ![]() 时y取最大值1,当x=
时y取最大值1,当x= ![]() 时y取最小值﹣1.
时y取最小值﹣1.
(1)求函数的解析式y=f(x);
(2)当x∈[ ![]() ,
, ![]() ]时.求函数y=f(x)的值域.
]时.求函数y=f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求b的值;
(2)用定义法证明函数f(x)在R上是减函数;
(3)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校设有甲、乙两个实验班,为了了解班级成绩,采用分层抽样的方法从甲、乙两班学生中分别抽取8名和6名测试他们的数学与英语成绩(单位:分),用![]() 表示,下面是乙班6名学生的测试分数:
表示,下面是乙班6名学生的测试分数: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,当学生的数学、英语成绩满足
,当学生的数学、英语成绩满足![]() ,且
,且![]() 时,该学生定为优秀生.
时,该学生定为优秀生.
(Ⅰ)已知甲班共有80名学生,用上述样本数估计乙班优秀生的数量;
(Ⅱ)从乙班抽出的上述6名学生中随机抽取3名,求至少有两名为优秀生的概率;
(Ⅲ)从乙班抽出的上述6名学生中随机抽取2名,其中优秀生数记为![]() ,求
,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:(1+4k)x﹣(2﹣3k)y+(2﹣14k)=0,圆C:x2+y2﹣6x﹣8y+9=0.
(1)判断直线l1与圆的位置关系,并证明你的结论;
(2)直线l2过直线l1的定点且l1⊥l2 , 若l1与圆C交与A,B两点,l2与圆C交与E,F两点,求AB+EF的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com