【题目】已知直线l1：（1+4k）x﹣（2﹣3k）y+（2﹣14k）=0，圆C：x2+y2﹣6x﹣8y+9=0．
（1）判断直线l1与圆的位置关系，并证明你的结论；
（2）直线l2过直线l1的定点且l1⊥l2 ， 若l1与圆C交与A，B两点，l2与圆C交与E，F两点，求AB+EF的最大值．
【答案】
（1）解：直线与圆相交
证明：直线方程可整理为（x﹣2y+2）+（4x+3y﹣14）k=0
所以 
解得 
所以直线过定点P（2，2）
圆C方程可整理为（x﹣3）2+（y﹣4）2=16
因为圆心C到点P（2，2）的距离d为 
由 
，所以直线与圆C相交
（2）解：设点C到直线AB，EF的距离分别为d1，d2（d1，d2≥0）
则 
又 
所以 
则 
= 
= 
= 
又因为 
所以 
（当且仅当 
时取到等号）
所以 
所以 
所以 
所以AB+EF的最大值为 
【解析】（1）直线方程可整理为（x﹣2y+2）+（4x+3y﹣14）k=0，可得直线过定点；求出圆心C到点P（2，2）的距离，与半径比较，可得可得直线l1与圆的位置关系；（2） ，利用基本不等式，即可求AB+EF的最大值．
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】设数列{an}的各项都为正数，其前n项和为Sn ， 已知4Sn=an2+2an ．
（1）求a1级数列{an}的通项公式；
（2）设数列{bn}前n项和为Tn ， 且bn= 
，若λTn＜n+（﹣1）n36对n∈N*恒成立，求实数λ的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
（
）过点
， 
、
分别为其左、右焦点， 
为坐标原点，点
为椭圆上一点， 
轴，且
的面积为
.
（Ⅰ）求椭圆
的离心率和方程；
（Ⅱ）设
、
是椭圆上两动点，若直线
的斜率为
，求
面积的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且 
=2csinA
（1）确定角C的大小；
（2）若c= 
，且△ABC的面积为 
，求a+b的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】河道上有一座圆拱桥，在正常水位时，拱圈最高点距水面9m，拱圈内水面宽22m．一条船在水面以上部分高6.5m，船顶部宽4m，故通行无阻．近日水位暴涨了2.7m，为此，必须加重舰载，降低船身，才能通过桥洞．试问船身至少应该降低多少？（精确到0.01，参考数据： 
） 
查看答案和解析>>
科目：高中数学 来源： 题型：
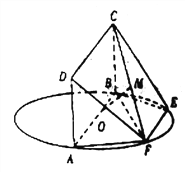
【题目】如图所示， 
为圆
的直径，点
， 
在圆
上， 
，矩形
所在的平面和圆
所在的平面互相垂直，且
， 
， 
.
（1）求证： 
平面
；
（2）设
的中点为
，求三棱锥
的体积
与多面体
的体积
之比的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某家具厂有方木料
，五合板
，准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
、五合板
；生产每个书橱需要方木枓
、五合板
.出售一张书桌可获利润
元，出售一个书橱可获利润
元，怎样安排生产可使所得利润最大？最大利润为多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
