
分析 利用函数的解析式对4个选项分别进行判断,即可得出结论.
解答 解:①∵f(-x)=-$\frac{x}{{x}^{2}+m}$=-f(x),∴函数f(x)是奇函数,
∵f(0)=0,∴函数f(x)过点(0,0),故正确;
②m>0,函数f(x)的极值点是x=±$\sqrt{m}$;,故不正确
③当m<0时,x=0,f(0)=0,x≠0,f(x)=$\frac{1}{x+\frac{m}{x}}$,函数f(x)在(-∞,0),(0,+∞)单调递减函数,故不正确;
④当m>0时,x=0,f(0)=0,x≠0,f(x)=$\frac{1}{x+\frac{m}{x}}$,大致图象如图所示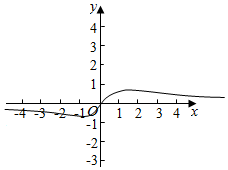
所以函数y=f(x)-a的零点个数可以是0个,1个,2个.正确.
故答案为:①④.
点评 本题考查函数的解析式与性质,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
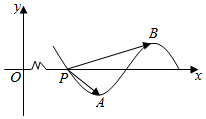 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)部分图象如图所示,点P为f(x)与x轴的交点,点A,B分别为f(x)图象的最低点与最高点,$\overrightarrow{PA}$•$\overrightarrow{PB}$=|$\overrightarrow{PA}$|2.
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)部分图象如图所示,点P为f(x)与x轴的交点,点A,B分别为f(x)图象的最低点与最高点,$\overrightarrow{PA}$•$\overrightarrow{PB}$=|$\overrightarrow{PA}$|2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | -32 | C. | 243 | D. | -243 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最小值无最大值 | B. | 有最大值无最小值 | ||
| C. | 既有最大值又有最小值 | D. | 既无最大值又无最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,设O为平行四边形ABCD所在平面外任意一点,E为OC的中点,若$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{OD}$+x$\overrightarrow{OB}$+y$\overrightarrow{OA}$,则x+y=-1.
如图,设O为平行四边形ABCD所在平面外任意一点,E为OC的中点,若$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{OD}$+x$\overrightarrow{OB}$+y$\overrightarrow{OA}$,则x+y=-1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在底面半径和高均为4的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点.若过直径CD与点E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )
如图,在底面半径和高均为4的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点.若过直径CD与点E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )| A. | 4 | B. | $2\sqrt{3}$ | C. | $2\sqrt{6}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -8 | C. | -9 | D. | -12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
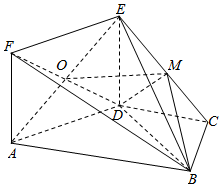 如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,CD=BC=$\frac{1}{2}$AB=1,AE∩DF=O,M为EC的中点.
如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,CD=BC=$\frac{1}{2}$AB=1,AE∩DF=O,M为EC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com