
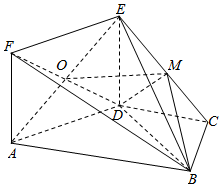
 如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,CD=BC=$\frac{1}{2}$AB=1,AE∩DF=O,M为EC的中点.
如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,CD=BC=$\frac{1}{2}$AB=1,AE∩DF=O,M为EC的中点.分析 (Ⅰ)推导出OM∥AC,由此能证明OM||平面ABCD.
(Ⅱ)取AB中点H,连接DH,则∠EHD为二面角D-AB-E的平面角,由此能求出二面角D-AB-E的正切值.
(Ⅲ)推导出BD⊥DA,从而BD⊥平面ADEF,由此得到∠BFD的余弦值即为所求.
解答 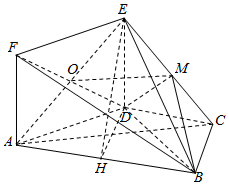 证明:(Ⅰ)∵O,M分别为EA,EC的中点,
证明:(Ⅰ)∵O,M分别为EA,EC的中点,
∴OM∥AC….(2分)
∵OM?平面ABCD,AC?平面ABCD….(3分)
∴OM||平面ABCD ….(4分)
解:(Ⅱ)取AB中点H,连接DH,EH∵DA=DB∴DH⊥AB,….(5分)
又EA=EB∴EH⊥AB….(6分)
∴∠EHD为二面角D-AB-E的平面角 ….(7分)
又DH=1,∴$tan∠EHD=\frac{ED}{DH}=\sqrt{2}$,
∴二面角D-AB-E的正切值为$\sqrt{2}$.….(8分)
(Ⅲ)∵DC=BC=1,∠BCD=90°,
∴$BD=\sqrt{2}$∵$AD=\sqrt{2},AB=2$.
∴BD⊥DA….(9分)
∵平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,BD?平面ABCD,
∴BD⊥平面ADEF….(10分)
∴∠BFD的余弦值即为所求…(11分)
在$Rt△BDF中,∠BDF=Rt∠,DF=2,BF=\sqrt{6}$,
∴$cos∠BFD=\frac{DF}{BF}=\frac{2}{{\sqrt{6}}}=\frac{{\sqrt{6}}}{3}$….(12分)
∴$BF与平面ADEF所成角的余弦值为\frac{{\sqrt{6}}}{3}$….(13分)
点评 本题考查线面平行的证明,考查二面角的正切值的求法,考查线面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
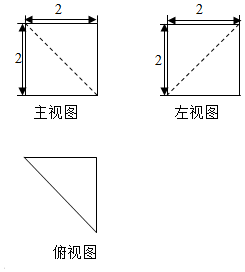 某空间几何体的三视图如图所示,则此几何体的体积是( )
某空间几何体的三视图如图所示,则此几何体的体积是( )| A. | $\frac{4}{3}$ | B. | $\frac{{4\sqrt{2}}}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{{8\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3,3 | B. | 3,-1 | C. | -1,3 | D. | -1,-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 转速x/(rad/s) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y/件 | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
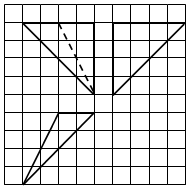 如图,网格纸上小正方形的边长为1,粗线画出的是某个多面体的三视图,若该多面体的所有顶点都在球O表面上,则球O的表面积是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某个多面体的三视图,若该多面体的所有顶点都在球O表面上,则球O的表面积是( )| A. | 36π | B. | 48π | C. | 56π | D. | 64π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 气温x(度) | 18 | 13 | 10 | -1 |
| 用电量y(度) | 24 | 34 | 38 | 64 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com