
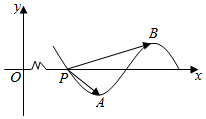
 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)部分图象如图所示,点P为f(x)与x轴的交点,点A,B分别为f(x)图象的最低点与最高点,$\overrightarrow{PA}$•$\overrightarrow{PB}$=|$\overrightarrow{PA}$|2.
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)部分图象如图所示,点P为f(x)与x轴的交点,点A,B分别为f(x)图象的最低点与最高点,$\overrightarrow{PA}$•$\overrightarrow{PB}$=|$\overrightarrow{PA}$|2.分析 (1)设函数f(x)的周期是T、P(a,0),由图象和周期性表示出A、B的坐标,根据向量的坐标运算和向量的数量积运算化简已知的式子,求出T后由周期公式求出ω;
(2)由(1)和x的范围求出f(x)、ωx+φ范围,利用正弦函数的性质求出f(x)的取值范围.
解答 解:(1)设函数f(x)=sin(ωx+φ)的周期是T,P(a,0),
则A(a+$\frac{T}{4}$,-1),B(a+$\frac{3T}{4}$,1),
∴$\overrightarrow{PA}$=($\frac{T}{4}$,-1),$\overrightarrow{PB}$=($\frac{3T}{4}$,1),
∵$\overrightarrow{PA}$•$\overrightarrow{PB}$=|$\overrightarrow{PA}$|2,∴$\frac{3{T}^{2}}{16}-1=\frac{{T}^{2}}{16}+1$,解得T=4,
由T=$\frac{2π}{ω}=4$得,ω=$\frac{π}{2}$;
(2)由(1)得,f(x)=sin($\frac{π}{2}$x+φ),
∵x∈[-1,1],∴$\frac{π}{2}x+φ∈[-\frac{π}{2}+φ,\frac{π}{2}+φ]$,
又0<φ<π,则$-\frac{π}{2}<-\frac{π}{2}+φ<\frac{π}{2},\frac{π}{2}<\frac{π}{2}+φ<\frac{3π}{2}$,
∴sin($\frac{π}{2}$x+φ)∈(-1,1),
即f(x)的取值范围是(-1,1).
点评 本题考查函数y=Asin(ωx+φ)的图象解析式的确定,向量数量积的坐标运算,以及正弦函数的性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{6}{7}$ | C. | $\frac{3}{10}$ | D. | $\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 | |
| 男生 | 800 | 450 | 200 |
| 女生 | 100 | 150 | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 202 | B. | 220 | C. | 222 | D. | 440 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 46 | B. | 23 | C. | 954 | D. | 317 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
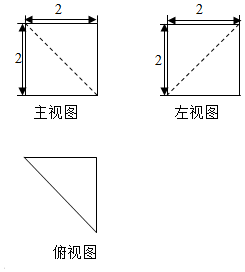 某空间几何体的三视图如图所示,则此几何体的体积是( )
某空间几何体的三视图如图所示,则此几何体的体积是( )| A. | $\frac{4}{3}$ | B. | $\frac{{4\sqrt{2}}}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{{8\sqrt{2}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com