
| 跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 | |
| 男生 | 800 | 450 | 200 |
| 女生 | 100 | 150 | 300 |
分析 (I)由题意利用分层抽样的性质列出方程,由此能求出n的值.
(II)由系统抽样得到的号码分别为100,225,350,475,其中100号为男生,设为A,而225,350,475都为女生,分别设为B1,B2,B3,由此利用列举法能求出从这4人中任选取2人,这两人均是女生的概率.
解答 (本小题满分10分)
解:(I)由题意得,$\frac{45}{800+100}=\frac{n}{800+450+200+100+150+300}$,
解得n=100.…(2分)
(II)由系统抽样得到的号码分别为100,225,350,475.…(4分)
其中100号为男生,设为A,而225,350,475都为女生,分别设为B1,B2,B3,
从这4人中任选取2人所有的基本事件为:
(AB1),(AB2),(AB3),(B1B2),(B1B3),(B2B3),共有6个.…(6分)
这两人均是女生的基本事件为(B1B2),(B1B3),(B2B3),共有3个.…(8分)
故从这4人中任选取2人,这两人均是女生的概率为$P=\frac{3}{6}=\frac{1}{2}$.…(10分)
点评 本题考查样本单元数的求法,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | “?x∈R,x≠|x|” | B. | “?x∈R,x=|x|” | C. | “?x∈R,x≠|x|” | D. | “?x∈R,x=-x” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | -2$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
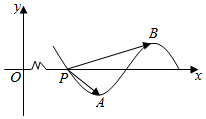 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)部分图象如图所示,点P为f(x)与x轴的交点,点A,B分别为f(x)图象的最低点与最高点,$\overrightarrow{PA}$•$\overrightarrow{PB}$=|$\overrightarrow{PA}$|2.
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)部分图象如图所示,点P为f(x)与x轴的交点,点A,B分别为f(x)图象的最低点与最高点,$\overrightarrow{PA}$•$\overrightarrow{PB}$=|$\overrightarrow{PA}$|2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在底面半径和高均为4的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点.若过直径CD与点E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )
如图,在底面半径和高均为4的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点.若过直径CD与点E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )| A. | 4 | B. | $2\sqrt{3}$ | C. | $2\sqrt{6}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com