
分析 (1)利用椭圆的定义,求出a,根据左焦点为F1(-1,0),得出c,求出b,即可椭圆C的方程;
(2)由(1)可知A(-2,0),B(2,0),设P(x0,y0),则直线PA的方程为y=$\frac{{y}_{0}}{{x}_{0}+2}$(x+2)①,直线PB的方程为y=$\frac{{y}_{0}}{{x}_{0}-2}$(x-2)②.将x=2代入①②,可得yD=$\frac{6{y}_{0}}{{x}_{0}+2}$,yE=$\frac{2{y}_{0}}{{x}_{0}-2}$,即求出D,E两点纵坐标的乘积是定值-9.
解答 解:(1)由椭圆的定义可得2a=$\sqrt{(1+1)^{2}+(\frac{3}{2})^{2}}$+$\frac{3}{2}$=4,
∴a=2,
∵c=1,∴b=$\sqrt{3}$,
∴椭圆C的方程是$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)由(1)可知A(-2,0),B(2,0),
设P(x0,y0),则直线PA的方程为y=$\frac{{y}_{0}}{{x}_{0}+2}$(x+2)①,直线PB的方程为y=$\frac{{y}_{0}}{{x}_{0}-2}$(x-2)②.
将x=4代入①②,可得yD=$\frac{6{y}_{0}}{{x}_{0}+2}$,yE=$\frac{2{y}_{0}}{{x}_{0}-2}$,
∴yD•yE=$\frac{6{y}_{0}}{{x}_{0}+2}$•$\frac{2{y}_{0}}{{x}_{0}-2}$=$\frac{12{{y}_{0}}^{2}}{{{x}_{0}}^{2}-4}$,
∵P(x0,y0)在椭圆上,
∴${{y}_{0}}^{2}$=-$\frac{3}{4}$(${{x}_{0}}^{2}$-4),
∴yD•yE=$\frac{12{{y}_{0}}^{2}}{{{x}_{0}}^{2}-4}$=-9
∴D,E两点纵坐标的乘积是定值-9.
点评 本题考查椭圆的定义与方程,考查D,E两点纵坐标的乘积是定值,考查学生的计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 | |
| 男生 | 800 | 450 | 200 |
| 女生 | 100 | 150 | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 46 | B. | 23 | C. | 954 | D. | 317 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
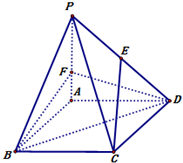 如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°.PA⊥面ABCD,且PA=3.F在棱PA上,且AF=1,E在棱PD上.
如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°.PA⊥面ABCD,且PA=3.F在棱PA上,且AF=1,E在棱PD上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com