
| A. | $\sqrt{3}$ | B. | -2$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | -$\sqrt{3}$ |
分析 根据条件及一个向量在另一个向量方向上投影的定义即可求出该投影的值.
解答 解:根据条件,$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为:
$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{|\overrightarrow{a}||\overrightarrow{b}|cos\frac{5π}{6}}{|\overrightarrow{b}|}$=$|\overrightarrow{a}|cos\frac{5π}{6}$=$-\sqrt{3}$.
故选D.
点评 考查向量长度和夹角的概念,以及一个向量在另一个向量方向上投影的定义.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{6}{7}$ | C. | $\frac{3}{10}$ | D. | $\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
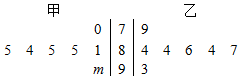
| A. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | B. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ | ||
| C. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$ | D. | $\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$的大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 身高x为解释变量,体重y为预报变量 | |
| B. | y与x具有正的线性相关关系 | |
| C. | 回归直线过样本点的中心($\overline x$,$\overline y$) | |
| D. | 若该大学某女生身高为170cm,则她的体重必为58.79kg |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 | |
| 男生 | 800 | 450 | 200 |
| 女生 | 100 | 150 | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 46 | B. | 23 | C. | 954 | D. | 317 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com