
| A. | 202 | B. | 220 | C. | 222 | D. | 440 |
分析 由题意可知:S1+S2+S3+…+S10=2200,2,a1,a2,…a10的“理想数”为$\frac{2+(2+{S}_{1})+(2+{S}_{2})+…+(2+{S}_{10})}{11}$,代入即可求得结果.
解答 解:由条件可得$\frac{{S}_{1}+{S}_{2}+…+{S}_{10}}{10}$=220,从而得S1+S2+S3+…+S10=2200,
又因为数列2,a1,a2,…a10的“理想数”为$\frac{2+(2+{S}_{1})+(2+{S}_{2})+…+(2+{S}_{10})}{11}$,
=$\frac{2×11+({S}_{1}+{S}_{2}+…{S}_{10})}{11}$,
=$\frac{2×11+2200}{11}$,
=202,
故答案选:A.
点评 本题主要考查了数列的求和问题.考查了学生根据已知条件解决实际问题的能力,考查了学生的创造性的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{2}$个单位 | B. | 向左平移$\frac{π}{2}$个单位 | ||
| C. | 向右平移$\frac{π}{4}$个单位 | D. | 向左平移$\frac{π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
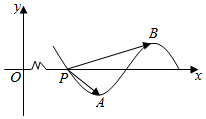 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)部分图象如图所示,点P为f(x)与x轴的交点,点A,B分别为f(x)图象的最低点与最高点,$\overrightarrow{PA}$•$\overrightarrow{PB}$=|$\overrightarrow{PA}$|2.
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)部分图象如图所示,点P为f(x)与x轴的交点,点A,B分别为f(x)图象的最低点与最高点,$\overrightarrow{PA}$•$\overrightarrow{PB}$=|$\overrightarrow{PA}$|2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | -32 | C. | 243 | D. | -243 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,设O为平行四边形ABCD所在平面外任意一点,E为OC的中点,若$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{OD}$+x$\overrightarrow{OB}$+y$\overrightarrow{OA}$,则x+y=-1.
如图,设O为平行四边形ABCD所在平面外任意一点,E为OC的中点,若$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{OD}$+x$\overrightarrow{OB}$+y$\overrightarrow{OA}$,则x+y=-1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com