
分析 将x=8代入函数的表达式,求出f(8)的值即可;画出函数f(x)的图象,结合图象求出a,b,c的范围,判断其大小即可.
解答 解:∵f(x)=$\left\{\begin{array}{l}{\frac{4}{x}+1,x≥4}\\{lo{g}_{2}x,0<x<4}\end{array}\right.$,
∴f(8)=$\frac{4}{8}$+1=$\frac{3}{2}$,
画出函数f(x)的图象,如图示: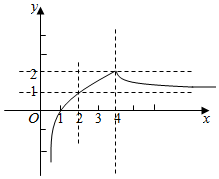 ,
,
若f′(b)<0,则b>4,
若f(a)=f(b)=c,则2<a<4,1<c<2,
故b>a>c,
故答案为:$\frac{3}{2}$,b>a>c.
点评 本题考查了求函数值问题,考查对数函数的性质以及数形结合思想,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 202 | B. | 220 | C. | 222 | D. | 440 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
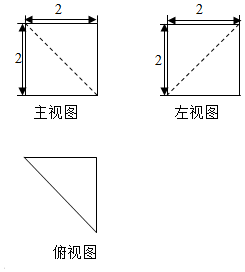 某空间几何体的三视图如图所示,则此几何体的体积是( )
某空间几何体的三视图如图所示,则此几何体的体积是( )| A. | $\frac{4}{3}$ | B. | $\frac{{4\sqrt{2}}}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{{8\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p假q假 | B. | p真q假 | C. | p假q真 | D. | p真q真 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 转速x/(rad/s) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y/件 | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | -2 | -1 | 0 | 1 | 2 |
| y | 5 | 4 | 2 | 2 | 1 |
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com