
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014-2015学年江苏省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分14分)已知函数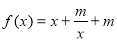 (
(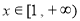 且
且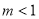 ).
).
(Ⅰ)用定义证明函数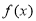 在
在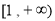 上为增函数;
上为增函数;
(Ⅱ)设函数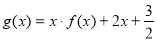 ,若[2, 5 ]是
,若[2, 5 ]是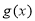 的一个单调区间,且在该区间上
的一个单调区间,且在该区间上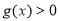 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市大兴区高三上学期期末考试理科数学试卷(解析版) 题型:解答题
已知椭圆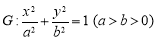 的离心率为
的离心率为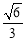 ,右焦点为
,右焦点为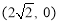 ,过原点
,过原点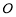 的直线
的直线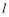 交椭圆于
交椭圆于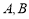 两点,线段
两点,线段 的垂直平分线交椭圆
的垂直平分线交椭圆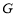 于点
于点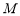 .
.
(Ⅰ)求椭圆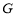 的方程;
的方程;
(Ⅱ)求证: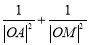 为定值,并求
为定值,并求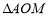 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市大兴区高三上学期期末考试理科数学试卷(解析版) 题型:选择题
如图,在复平面内,复数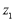 和
和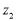 对应的点分别是
对应的点分别是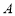 和
和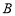 ,则
,则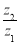 等于
等于

(A)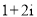 (B)
(B)
(C)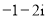 (D)
(D)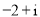
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市朝阳区高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题满分13分)退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势.某机构为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600人进行调查,并按年龄层次[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]绘制频率分布直方图,如图所示.若规定年龄分布在[20,40)岁的人为“青年人”,[40,60)为“中年人”, [60,80]为“老年人”.
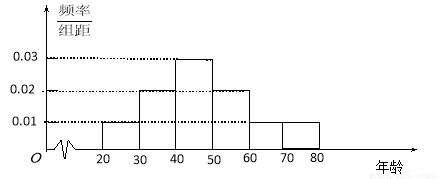
(Ⅰ)若每一组数据的平均值用该区间中点值来代替,试估算所调查的600人的平均年龄;
(Ⅱ)将上述人口分布的频率视为该城市在20-80年龄段的人口分布的概率.从该城市20-80年龄段市民中随机抽取3人,记抽到“老年人”的人数为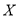 ,求随机变量
,求随机变量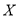 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市朝阳区高三上学期期末考试理科数学试卷(解析版) 题型:选择题
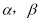 表示不重合的两个平面,
表示不重合的两个平面,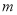 ,
,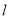 表示不重合的两条直线.若
表示不重合的两条直线.若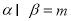 ,
,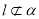 ,
,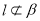 ,则“
,则“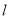 ∥
∥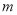 ”是“
”是“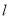 ∥
∥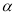 且
且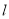 ∥
∥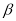 ”的( )
”的( )
A.充分且不必要条件
B.必要且不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高一上学期第二次月考数学试卷(解析版) 题型:解答题
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度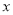 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当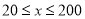 时,车流速度
时,车流速度 是车流密度x的一次函数.
是车流密度x的一次函数.
(Ⅰ)当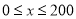 时,求函数
时,求函数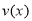 的表达式;
的表达式;
(Ⅱ)当车流密度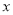 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)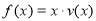 可以达到最大,并求出最大值(精确到1辆/小时)。
可以达到最大,并求出最大值(精确到1辆/小时)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com