
【题目】对于函数y=3sin(2x+ ![]() ),
),
(1)求振幅、初相和最小正周期;
(2)简述此函数图象是怎样由函数y=sinx的图象作变换得到的.
【答案】
(1)解:对于函数y=3sin(2x+ ![]() ),它的振幅为3,初相为
),它的振幅为3,初相为 ![]() ,最小正周期为
,最小正周期为 ![]() =π
=π
(2)解:把函数y=sinx的图象向左平移 ![]() 个单位,可得y=sin(x+
个单位,可得y=sin(x+ ![]() )的图象;
)的图象;
再把横坐标变为原来的 ![]() 倍,可得y=sin(2x+
倍,可得y=sin(2x+ ![]() )的图象;
)的图象;
再把纵坐标变为原来的3倍,可得y=3sin(2x+ ![]() )的图象
)的图象
【解析】y=Asin(ωx+φ)的图象变换规律,再根据y=Asin(ωx+φ)的振幅、周期、初相的定义,得出结论.
【考点精析】关于本题考查的函数y=Asin(ωx+φ)的图象变换,需要了解图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能得出正确答案.
的图象才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 为增函数,对任意
为增函数,对任意![]() 都有
都有![]() (
(![]() 为常数)
为常数)
(1)判断![]() 为何值时,
为何值时,![]() 为奇函数,并证明;
为奇函数,并证明;
(2)设![]() ,
,![]() 是
是![]() 上的增函数,且
上的增函数,且![]() ,若不等式
,若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)若![]() ,
,![]() ,
,![]() 为
为![]() 的前
的前![]() 项和,求正整数
项和,求正整数![]() ,使得对任意
,使得对任意![]() 均有
均有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作直线
作直线![]() 分别交
分别交![]() 轴的正半轴于
轴的正半轴于![]() 两点.
两点.
(Ⅰ)当![]() 取最小值时,求出最小值及直线
取最小值时,求出最小值及直线![]() 的方程;
的方程;
(Ⅱ)当![]() 取最小值时,求出最小值及直线
取最小值时,求出最小值及直线![]() 的方程;
的方程;
(Ⅲ)当![]() 取最小值时,求出最小值及直线
取最小值时,求出最小值及直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年12月,华中地区数城市空气污染指数“爆表”,此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)(I)利用(1)所求的回归方程,预测该市车流量为12万辆时![]() 的浓度;(II)规定:当一天内
的浓度;(II)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是![]() ,其中
,其中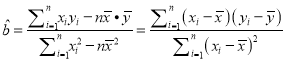 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用分层抽样的方法从某校学生中抽取一个容量为60的样本,其中高二年级抽取20人,高三年级抽取25人,已知该校高一年级共有800人,则该校学生总数为人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C经过A(0,1),B(3,4),C(6,1)三点.
(1)求圆C的方程;
(2)若圆C与直线x﹣y+a=0交于A,B两点,且OA⊥OB,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com