
【题目】过点![]() 作直线
作直线![]() 分别交
分别交![]() 轴的正半轴于
轴的正半轴于![]() 两点.
两点.
(Ⅰ)当![]() 取最小值时,求出最小值及直线
取最小值时,求出最小值及直线![]() 的方程;
的方程;
(Ⅱ)当![]() 取最小值时,求出最小值及直线
取最小值时,求出最小值及直线![]() 的方程;
的方程;
(Ⅲ)当![]() 取最小值时,求出最小值及直线
取最小值时,求出最小值及直线![]() 的方程.
的方程.
【答案】(Ⅰ)答案见解析;(Ⅱ)答案见解析;(Ⅲ)答案见解析.
【解析】试题分析:(Ⅰ)设![]() . 设直线方程为
. 设直线方程为![]() ,代入
,代入![]() 得
得![]() ,
,
由假能诺丁山可得![]() ,此时
,此时![]() ,而斜率
,而斜率![]() .,由点斜式可得直线方程
.,由点斜式可得直线方程
(Ⅱ)![]() 由基本不等式可求
由基本不等式可求![]() 的最小值,此时
的最小值,此时![]() ,可求斜率
,可求斜率![]() ,则直线方程可求
,则直线方程可求
(Ⅲ)设直线![]() ,则
,则![]() .
.
则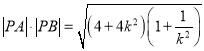 =
= ,
,
当且仅当![]() ,时,
,时, ![]() 取最小值,又∵
取最小值,又∵![]() ,可得
,可得![]() ,则直线方程可求
,则直线方程可求
试题解析:设![]() .
.
(Ⅰ)设直线方程为![]() ,代入
,代入![]() 得
得![]() ,
,
得![]() ,从而
,从而![]() ,此时
,此时![]() ,
, ![]() .
.
∴方程为![]() .
.
(Ⅱ)![]()
![]() ,
,
此时![]() ,
, ![]() .
.
∴方程为![]() .
.
(Ⅲ)设直线![]() ,分别令
,分别令![]() ,得
,得![]() .
.
则 =
=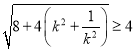 ,
,
当且仅当![]() ,即
,即![]() 时,
时, ![]() 取最小值,又∵
取最小值,又∵![]() ,
,
∴![]() ,这时
,这时![]() 的方程为
的方程为![]() .
.
【点击】本题考查三角形的面积公式、两点间的距离公式及基本不等式的应用,解题时要注意应用基本不等式时需满足的条件.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() :
:![]() ,过焦点
,过焦点![]() 斜率大于零的直线
斜率大于零的直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,且与其准线交于点
两点,且与其准线交于点![]() .
.

(Ⅰ)若线段![]() 的长为
的长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)在![]() 上是否存在点
上是否存在点![]() ,使得对任意直线
,使得对任意直线![]() ,直线
,直线![]() ,
,![]() ,
,![]() 的斜率始终成等差数列,若存在求点
的斜率始终成等差数列,若存在求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 分别与圆
分别与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.

(Ⅰ)若![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(Ⅱ)若直线![]() 过点
过点![]() ,证明:
,证明:![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 为实常数.
为实常数.
(Ⅰ)设![]() ,当
,当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,直线
时,直线![]() 、
、![]() 与函数
与函数![]() 、
、![]() 的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.
的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.
求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
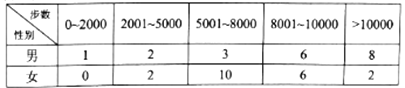
(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
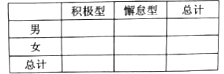
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
 附:
附: 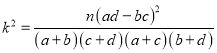 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人玩猜数字游戏,先由甲心中任想一个数字记为![]() ,再由乙猜甲刚才想的数字,把乙猜的数字记为
,再由乙猜甲刚才想的数字,把乙猜的数字记为![]() ,且
,且![]() 、
、![]() .若
.若![]() ,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com