
分析 (Ⅰ)根据题意以及点到直线的距离公式求得圆的半径,从而求得圆C的标准方程;
(Ⅱ)由 点(-1,-1)在圆内,且弦长为2<$2\sqrt{5}$,判断应有两条直线,然后分类讨论当l斜率存在时和当l斜率不存在时,求出直线l的方程即可.
解答 解:(Ⅰ) 圆的半径为圆心(1,2)到切线2x+y+1=0的距离,
即r=$\frac{|2+2+1|}{\sqrt{{2}^{2}+1}}$=$\sqrt{5}$,
∴圆C的标准方程为(x-1)2+(y-2)2=5;
(Ⅱ) 点(-1,-1)在圆内,且弦长为2<$2\sqrt{5}$,∴应有两条直线.
①当l斜率存在时,设l:y+1=k(x+1),即kx-y+k-1=0.
由弦长公式,$2=2\sqrt{{r}^{2}-{d}^{2}}=2\sqrt{5-{d}^{2}}$,得d=2.
∴圆心到直线l的距离$d=\frac{|2k-3|}{\sqrt{{k}^{2}+1}}=2$,解得$k=\frac{5}{12}$,此时l:5x-12y-7=0.
②当l斜率不存在时,l:x=-1,也符合题意.
∴直线方程为:5x-12y-7=0或x=-1.
点评 本题主要考查直线和圆的位置关系,点到直线的距离公式的应用以及弦长公式,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得${3^{x_0}}≤0$ | |
| B. | ?x∈R+,lgx>0 | |
| C. | “$x=\frac{π}{6}$”是“$cosx=\frac{{\sqrt{3}}}{2}$”的必要不充分条件 | |
| D. | “x=1”是“x≥1”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
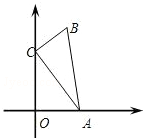 如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离是1+$\sqrt{2}$.
如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离是1+$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 4 | C. | 5 | D. | -3或4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com