
有一块直角三角形木板,如图所示,∠C=90°,AB=5 cm,BC=3 cm,AC=4 cm,根据需要,要把它加工成一个面积最大的正方形木板,设计一个方案,应怎样裁才能使正方形木板面积最大,并求出这个正方形木板的边长.
科目:高中数学 来源:2016届云南省高一下学期期末考试数学试卷(解析版) 题型:选择题
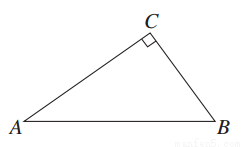
在三棱柱 中,已知
中,已知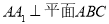 ,
, ,此三棱柱各个顶点都在一个球面上,则球的体积为( ).
,此三棱柱各个顶点都在一个球面上,则球的体积为( ).
A.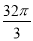 B.
B. C.
C.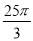 D.
D.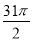
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-2直线与圆的位置关系(解析版) 题型:解答题
如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.

(1)求证:直线AB是⊙O的切线;
(2)若AD=2,且tan∠ACD=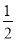 ,求⊙O的半径r的长.
,求⊙O的半径r的长.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-2直线与圆的位置关系(解析版) 题型:填空题
如图所示,AB是⊙O的直径,直线CB切⊙O于点B,直线CD切⊙O于点D,CD交BA的延长线于点E.若AB=3,ED=2,则BC的长为________.
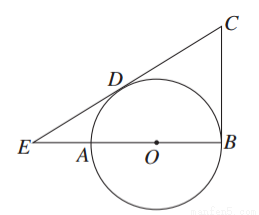
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-1相似三角形判定及性质(解析版) 题型:解答题
如图,△ABC中,AB=AC,∠BAC=90°,AE=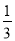 AC,BD=
AC,BD=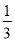 AB,点F在BC上,且CF=
AB,点F在BC上,且CF=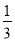 BC.求证:
BC.求证:
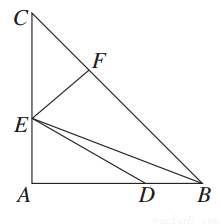
(1)EF⊥BC;
(2)∠ADE=∠EBC.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-1相似三角形判定及性质(解析版) 题型:选择题
Rt△ABC中,∠C=90°,CD⊥AB于D,若BD∶AD=3∶2,则△ACD与△CBD的相似比为( )
A.2∶3 B.3∶2 C.9∶4 D. ∶3
∶3
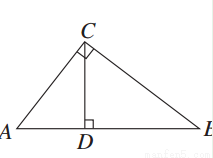
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-2用样本估计总体(解析版) 题型:解答题
已知某单位有50名职工,现要从中抽取10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组,按各组内抽取的编号依次增加5进行系统抽样.
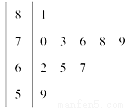
(1)若第5组抽出的号码为22,写出所有被抽出职工的号码;
(2)分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示,求该样本的方差;
(3)在(2)的条件下,从这10名职工中随机抽取两名体重不轻于73公斤(≥73公斤)的职工,求体重为76公斤的职工被抽取到的概率.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-9圆锥曲线的综合问题(解析版) 题型:选择题
若双曲线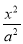 -
-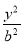 =1(a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶5的两段,则此双曲线的离心率为( )
=1(a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶5的两段,则此双曲线的离心率为( )
A.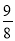 B.
B.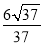 C.
C.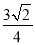 D.
D.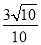
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com