练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

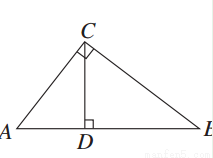
    Rt△ABC中，∠C＝90°，CD⊥AB于D，若BD∶AD＝3∶2，则△ACD与△CBD的相似比为(　　)

    A．2∶3 B．3∶2 C．9∶4 D．∶3

     

     

    D

    【解析】如图Rt△ABC中，由CD⊥AB及射影定理知，

    CD2＝AD·BD，即＝，

    又∵∠ADC＝∠BDC＝90°，

    ∴△ACD∽△CBD．

    ∵BD∶AD＝3∶2

    ∴令BD＝3t，AD＝2t，

    则CD2＝6t2，即CD＝t，∴＝＝．

    故△ACD与△CBD的相似比为∶3．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2016届云南省高一下学期期中考试数学试卷（解析版） 题型：解答题

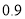    某种汽车购买时费用为万元，每年应交保险费，养路费，保险费共 万元，汽车的维修费为：第一年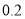万元，第二年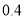万元，第三年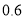万元，……，依次成等差数列逐年递增.

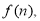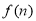    （1）设使用年该车的总费用(包括购车费用)为试写出的表达式；

    （2）求这种汽车使用多少年报废最合算（即该车使用多少年平均费用最少）.

     

    查看答案和解析>>

    科目：高中数学 来源：2016届上海市高一下学期期末考试数学试卷（解析版） 题型：填空题

    计算 .

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：选4-1-1相似三角形判定及性质（解析版） 题型：解答题

    有一块直角三角形木板，如图所示，∠C＝90°，AB＝5 cm，BC＝3 cm，AC＝4 cm，根据需要，要把它加工成一个面积最大的正方形木板，设计一个方案，应怎样裁才能使正方形木板面积最大，并求出这个正方形木板的边长．

     

     

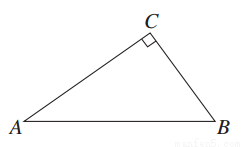
    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：选4-1-1相似三角形判定及性质（解析版） 题型：填空题

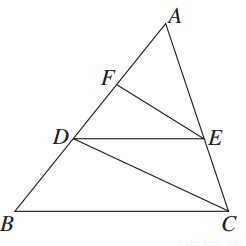
    如图，在△ABC中，DE∥BC，EF∥CD，若BC＝3，DE＝2，DF＝1，则BD的长为________，AB的长为________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：9-4算法初步（解析版） 题型：填空题

    下图为某算法的程序框图，则程序运行后输出的结果是________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：9-4算法初步（解析版） 题型：选择题

    如图给出的是计算1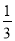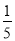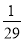＋＋＋…＋的值的一个程序框图，则图中执行框中的①处和判断框中的②处应填的语句分别是(　　)

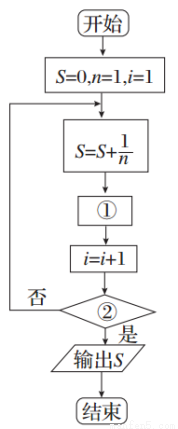
    A．n＝n＋2，i＝15?

    B．n＝n＋2，i>15?

    C．n＝n＋1，i＝15?

    D．n＝n＋1，i>15?

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：9-2用样本估计总体（解析版） 题型：选择题

    有一个容量为200的样本，其频率分布直方图如图所示．根据样本的频率分布直方图估计，样本数据落在区间[10,12)内的频数为(　　)

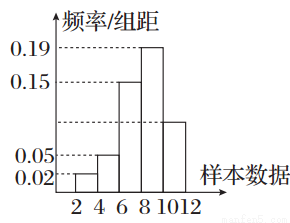
    A．18 B．36 C．54 D．72

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-8曲线与方程（解析版） 题型：填空题

    设抛物线C1的方程为y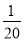＝x2，它的焦点F关于原点的对称点为E．若曲线C2上的点到E、F的距离之差的绝对值等于6，则曲线C2的标准方程为________．

     

    查看答案和解析>>

    同步练习册答案