
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若存在![]() ,使得不等式
,使得不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)求出函数![]() 的定义域和导数,由
的定义域和导数,由![]() 得出
得出![]() 和
和![]() ,然后对
,然后对![]() 和
和![]() 的大小关系进行分类讨论,分析导数符号,可得出函数
的大小关系进行分类讨论,分析导数符号,可得出函数![]() 的单调增区间和减区间;
的单调增区间和减区间;
(2)由![]() ,得出
,得出![]() ,得出
,得出![]() ,构造函数
,构造函数![]() ,将问题转化为
,将问题转化为![]() ,其中
,其中![]() ,然后利用导数求出函数
,然后利用导数求出函数![]() 在区间
在区间![]() 上的最小值,可得出实数
上的最小值,可得出实数![]() 的取值范围.
的取值范围.
(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]() .
.
当![]() 时,令
时,令![]() ,可得
,可得![]() 或
或![]() .
.
①当![]() 时,即当
时,即当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,
,
此时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
②当![]() 时,即当
时,即当![]() 时,
时,
令![]() ,得
,得![]() 或
或![]() ;令
;令![]() ,得
,得![]() .
.
此时,函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;
;
③当![]() 时,即当
时,即当![]() 时,
时,
令![]() ,得
,得![]() 或
或![]() ;令
;令![]() ,得
,得![]() .
.
此时,函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(2)由题意![]() ,可得
,可得![]() ,可得
,可得![]() ,其中
,其中![]() .
.
构造函数![]() ,
,![]() ,则
,则![]() .
.
![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,函数![]() 在
在![]() 或
或![]() 处取得最小值,
处取得最小值,
![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】推进垃圾分类处理,是落实绿色发展理念的必然选择,也是打赢污染防治攻坚战的重要环节.为了解居民对垃圾分类的了解程度,某社区居委会随机抽取1000名社区居民参与问卷测试,并将问卷得分绘制频率分布表如下:
得分 |
|
|
|
|
|
|
|
男性人数 | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性人数 | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)从该社区随机抽取一名居民参与问卷测试,试估计其得分不低于60分的概率;
(2)将居民对垃圾分类的了解程度分为“比较了解“(得分不低于60分)和“不太了解”(得分低于60分)两类,完成![]() 列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
不太了解 | 比较了解 | |
男性 | ||
女性 |
(3)从参与问卷测试且得分不低于80分的居民中,按照性别进行分层抽样,共抽取10人,连同![]() 名男性调查员一起组成3个环保宜传队.若从这
名男性调查员一起组成3个环保宜传队.若从这![]() 中随机抽取3人作为队长,且男性队长人数占的期望不小于2.求
中随机抽取3人作为队长,且男性队长人数占的期望不小于2.求![]() 的最小值.
的最小值.
附:![]()
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名同学参加一项射击比赛游戏,其中任何一人每射击一次击中目标得2分,未击中目标得0分.若甲、乙两人射击的命中率分别为![]() 和
和![]() ,且甲、乙两人各射击一次得分之和为2的概率为
,且甲、乙两人各射击一次得分之和为2的概率为![]() .假设甲、乙两人射击互不影响,则
.假设甲、乙两人射击互不影响,则![]() 值为( )
值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级三个班共有学生120名,这三个班的男女生人数如下表所示,已知在全年级中随机抽取1名学生,抽到二班女生的概率是0.2,则![]() _________.现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为________.
_________.现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为________.
一班 | 二班 | 三班 | |
女生人数 | 20 |
|
|
男生人数 | 20 | 20 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间[0,1]上的函数y=f(x)的图象如图所示.对满足0<x1<x2<1的任意x1,x2,给出下列结论:
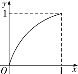
①f(x1)-f(x2)>x1-x2;
②f(x1)-f(x2)<x1-x2;
③x2f(x1)>x1f(x2);
④![]() .
.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]()
![]() ,对于
,对于![]() ,
,![]() ,定义A与B的差为
,定义A与B的差为![]() ;A与B之间的距离为
;A与B之间的距离为![]() .
.
(I)若![]() ,试写出所有可能的A,B;
,试写出所有可能的A,B;
(II)![]() ,证明:
,证明:
(i)![]() ;
;
(ii)![]()
![]()
![]() 三个数中至少有一个是偶数;
三个数中至少有一个是偶数;
(III)设![]() ,
,![]() 中有m(
中有m(![]() ,且为奇数)个元素,记P中所有两元素间距离的平均值为
,且为奇数)个元素,记P中所有两元素间距离的平均值为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx﹣x+1,g(x)=ex﹣ax,a∈R.
(Ⅰ)求f(x)的最小值;
(Ⅱ)若g(x)≥1在R上恒成立,求a的值;
(Ⅲ)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P ABC中,PA⊥平面ABC,![]() Q是BC边上的一个动点,且直线PQ与面ABC所成角的最大值为
Q是BC边上的一个动点,且直线PQ与面ABC所成角的最大值为![]() 则该三棱锥外接球的表面积为( )
则该三棱锥外接球的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com