
用分层抽样方法从高中三个年级的相关人员中抽取若干人组成研究小组,有关数据见下表:(单位:人)
| 年级 | 相关人数 | 抽取人数 |
| 高一 | 99 | 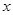 |
| 高二 | 27 | 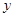 |
| 高三 | 18 | 2 |
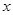 ,
,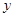 ;
;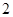 人,求这二人都来自高二年级的概率.
人,求这二人都来自高二年级的概率. (Ⅰ)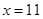 ,
,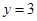 ;(Ⅱ)
;(Ⅱ)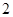 人都来自高二的概率为
人都来自高二的概率为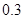 .
.
解析试题分析:(Ⅰ)分层抽样,实质上就是按比例抽样,所以根据比例式 ,即可得
,即可得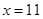 ,
,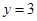 .
.
(Ⅱ)将高二、高三年级抽取的人分别用字母表示出来,可记为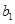 ,
,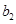 ,
,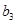 和
和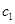 ,
,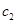 ,然后将所有基本事件(即可能出现的结果)一一列出,数出都来自高二年级的个数,由古典概型的概率公式即得.
,然后将所有基本事件(即可能出现的结果)一一列出,数出都来自高二年级的个数,由古典概型的概率公式即得.
试题解析:(Ⅰ)由题意可得  ,所以
,所以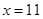 ,
,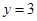 . 4分
. 4分
(Ⅱ)记从高二年级抽取的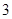 人为
人为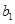 ,
,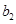 ,
,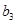 ,从高三年级抽取的
,从高三年级抽取的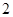 人为
人为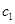 ,
,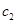 ,
,
则从这两个年级中抽取的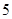 人中选
人中选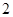 人的基本事件有:
人的基本事件有: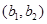 ,
,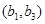 ,
,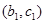 ,
,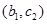 ,
,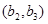 ,
,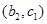 ,
,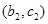 ,
,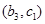 ,
,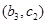 ,
,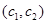 共
共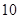 种. 8分
种. 8分
设选中的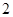 人都来自高二的事件为
人都来自高二的事件为 ,
,
则 包含的基本事件有:
包含的基本事件有: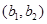 ,
,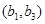 ,
,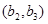 共
共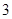 种. 11分
种. 11分
因此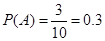 .
.
故选中的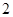 人都来自高二的概率为
人都来自高二的概率为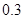 . 13分
. 13分
考点:1、分层抽样;2、古典概型.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
| | 喜欢 | 不喜欢[来源:学科网ZXXK] | 合计 |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中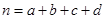 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示
(Ⅰ)求上图中 的值;
的值;
(Ⅱ)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);
(Ⅲ)由上图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作。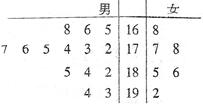
(I)求男生成绩的中位数及女生成绩的平均值;
(II)如果用分层抽样的方法从“甲部门”人选和“乙部门”人选中共选取5人,再从这5人中选2人,那么至少有一人是“甲部门”人选的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校有教职工 人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
(Ⅰ)随机抽取一人,是35岁以下的概率为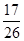 ,求
,求 的值;
的值;
(Ⅱ)从50岁以上的6人中随机抽取两人,求恰好只有一位是研究生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念性指数值,交通指数取值范围为0~10,分为五个级别,0~2 畅 通;2~4 基本畅通;4~6 轻度拥堵;6~8 中度拥堵;8~10 严重拥堵 早高峰时段,从昆明市交通指挥中心随机选取了二环以内的50个交通路段,依据其交通指数数据绘制的直方图如图 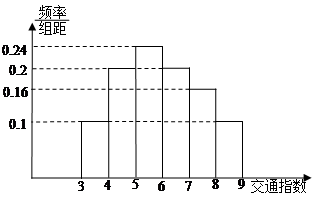
(1)据此估计,早高峰二环以内的三个路段至少有一个是严重拥堵的概率是多少?
(2)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟;中度拥堵为42分钟;严重拥堵为60分钟,求此人所用时间的数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组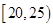 ,第2组
,第2组 ,第3组
,第3组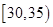 ,第4组
,第4组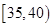 ,第5组
,第5组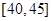 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班样本的方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com