
某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
| | 喜欢 | 不喜欢[来源:学科网ZXXK] | 合计 |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中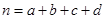 )
) (1)有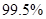 的把握认为喜欢“人文景观”景点与年龄有关;(2)
的把握认为喜欢“人文景观”景点与年龄有关;(2)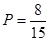 .
.
解析试题分析:本题主要考查实际问题中的独立性检验、随机事件的概率、分层抽样等数学知识,考查计算能力,综合分析问题解决问题的能力.第一问,根据已知的表格读出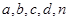 的值,利用
的值,利用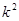 的公式计算,再与
的公式计算,再与 作比较,得到概率值判断相关性;第二问,先用分层抽样得出抽取的6人中“大于40岁”和“20岁至40岁”的分别多少人,用字母代表,在这6人中选2人,所有情况可以用字母一一列出共15种,其中恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的情况有8种,所以概率为
作比较,得到概率值判断相关性;第二问,先用分层抽样得出抽取的6人中“大于40岁”和“20岁至40岁”的分别多少人,用字母代表,在这6人中选2人,所有情况可以用字母一一列出共15种,其中恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的情况有8种,所以概率为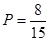 .
.
试题解析:(1)由公式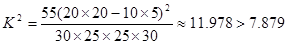
所以有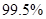 的把握认为喜欢“人文景观”景点与年龄有关 5分
的把握认为喜欢“人文景观”景点与年龄有关 5分
(2)设所抽样本中有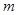 个“大于40岁”市民,则
个“大于40岁”市民,则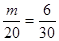 ,得
,得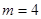 人
人
所以样本中有4个“大于40岁”的市民,2个“20岁至40岁”的市民,分别记作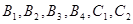 ,从中任选2人的基本事件有
,从中任选2人的基本事件有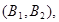
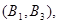
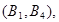
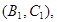

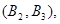

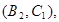
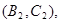
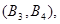
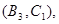
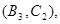
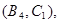
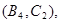
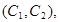 共15个 9分
共15个 9分
其中恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的事件有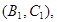

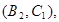
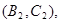
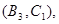
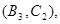
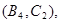 共8个
共8个
所以恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的概率为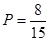 12分
12分
考点:1.独立性检验;2.随机事件的概率;3.分层抽样.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次.根据年龄将大众评委分为五组,各组的人数如下:
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 抽取人数 | | 6 | | | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
| | 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |

| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某社团组织20名志愿者利用周末和节假日参加社会公益活动,志愿者中,年龄在20至40岁的有12人,年龄大于40岁的有8人.
(1)在志愿者中用分层抽样方法随机抽取5名,年龄大于40岁的应该抽取几名?
(2)上述抽取的5名志愿者中任取2名,求取出的2人中恰有1人年龄大于40岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
| 应该取消 | 应该保留 | 无所谓 | ||
| 在校学生 | 2100人 | 120人 | y人 | ||
| 社会人士 | 600人 | x人 | z人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客需求,为此,某市公交公司在某站台的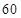 名候车乘客中随机抽取
名候车乘客中随机抽取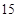 人,将他们的候车时间作为样本分成
人,将他们的候车时间作为样本分成 组,如下表所示(单位:min):
组,如下表所示(单位:min):
| 组别 | 候车时间 | 人数 |
| 一 |  |  |
| 二 |  | 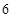 |
| 三 |  |  |
| 四 |  |  |
| 五 |  |  |
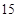 名乘客的平均候车时间;
名乘客的平均候车时间;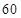 名乘客中候车时间少于
名乘客中候车时间少于 分钟的人数;
分钟的人数;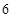 人中选
人中选 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100),分别加以统计,得到如图所示的频率分布直方图。

(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数;
(2)若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”;“25周岁以下组”中日平均生产不足60件的称为“菜鸟”。从样本中的“生产能手”和”菜鸟”中任意抽取2人,求这2人日平均生产件数之和X的分布列及期望。(“生产能手”日平均生产件数视为95件,“菜鸟”日平均生产件数视为55件)。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
用分层抽样方法从高中三个年级的相关人员中抽取若干人组成研究小组,有关数据见下表:(单位:人)
| 年级 | 相关人数 | 抽取人数 |
| 高一 | 99 | 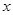 |
| 高二 | 27 | 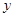 |
| 高三 | 18 | 2 |
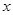 ,
,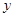 ;
;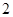 人,求这二人都来自高二年级的概率.
人,求这二人都来自高二年级的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
口袋中有n(n∈N*)个白球,3个红球.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为X,若P(X=2)=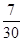 求:
求:
(1)n的值;
(2)X的概率分布与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com