
【题目】某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用下图的两条线段表示;该商品在30天内日销售量Q(件)与时间t(天)之间的关系Q=﹣t+40. 
(1)根据提供的图象,写出该商品每件的销售价格P与时间t的函数关系式;
(2)问这30天内,哪天的销售额最大,最大是多少?(销售额=销售价格×销售量)
【答案】
(1)解:当0<t<25时,设P=kt+b,则 ![]()
∴ ![]() ∴P=t+20
∴P=t+20
当25≤t≤30时,设P=mt+n,则 ![]() ,∴
,∴ ![]() ,
,
∴P=﹣t+100
∴ ![]()
(2)解:设销售额为S元
当0<t<25时,S=PQ=(t+20)(﹣t+40)=﹣t2+20t+800=﹣(t﹣10)2+900
∴当t=10时,Smax=900
当25≤t≤30时,S=PQ=(100﹣t)(﹣t+40)=t2﹣140t+4000=(t﹣70)2﹣900
∴当t=25时,Smax=1125>900
综上所述,第25天时,销售额最大为1125元.
【解析】(1)根据图象可知,每件商品的销售价格P与时间t的函数关系式满足一次函数,根据图象中所提供的点进行求解(2)由日销售金额=每件的销售价格×日销售量可得,且由确表格中所提供的数据可知Q=t﹣40,从而结合(1)可得 ![]() ,利用二次函数的性质进行求解最大值
,利用二次函数的性质进行求解最大值


科目:高中数学 来源: 题型:
【题目】潍坊文化艺术中心的观光塔是潍坊市的标志性建筑,某班同学准备测量观光塔![]() 的高度
的高度![]() (单位:米),如图所示,垂直放置的标杆
(单位:米),如图所示,垂直放置的标杆![]() 的高度
的高度![]() 米,已知
米,已知![]() ,
, ![]() .
.
(1)该班同学测得![]() 一组数据:
一组数据: ![]() ,请据此算出
,请据此算出![]() 的值;
的值;
(2)该班同学分析若干测得的数据后,发现适当调整标杆到观光塔的距离![]() (单位:米),使
(单位:米),使![]() 与
与![]() 的差较大,可以提高测量精确度,若观光塔高度为136米,问
的差较大,可以提高测量精确度,若观光塔高度为136米,问![]() 为多大时,
为多大时, ![]() 的值最大?
的值最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数,
是奇函数,
(1)求实数a的值;
(2)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求实数k的取值范围;
(3)设关于x的方程f(4x﹣b)+f(﹣2x+1)=0有实数根,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() ,点P
,点P![]() ,过右焦点F作与y轴不垂直的直线l交椭圆C于A,B两点.
,过右焦点F作与y轴不垂直的直线l交椭圆C于A,B两点.
(Ⅰ )求椭圆C的离心率;
(Ⅱ )求证:以坐标原点O为圆心与PA相切的圆,必与直线PB相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
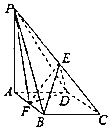
【题目】如图:在四棱锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥底面ABCD,E是PC中点,F是AB中点.
(Ⅰ)求证:BE∥平面PDF;
(Ⅱ)求直线PD与平面PFB所成角的正切值;
(Ⅲ)求三棱锥P﹣DEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() 则不等式f(x)>f(1)的解集是( )
则不等式f(x)>f(1)的解集是( )
A.(﹣3,1)∪(3,+∞)
B.(﹣3,1)∪(2,+∞)
C.(﹣1,1)∪(3,+∞)
D.(﹣∞,﹣3)∪(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣4x+a+3,a∈R.
(1)若函数y=f(x)的图象与x轴无交点,求a的取值范围;
(2)若函数y=f(x)在[﹣1,1]上存在零点,求a的取值范围;
(3)设函数g(x)=bx+5﹣2b,b∈R.当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使得f(x1)=g(x2),求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ),焦点
),焦点![]() 到准线的距离为
到准线的距离为![]() ,过点
,过点![]()
![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于点
于点![]() (点
(点![]() 在第一象限).
在第一象限).
(Ⅰ)若点![]() 焦点
焦点![]() 重合,且弦长
重合,且弦长![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)若点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 交x轴于点
交x轴于点![]() ,且
,且![]() ,求证:点B的坐标是
,求证:点B的坐标是![]() ,并求点
,并求点![]() 到直线
到直线![]() 的距离
的距离![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com