
已知椭圆C: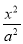 +
+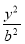 =1
=1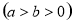 的离心率为
的离心率为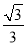 ,左焦点为F(-1,0),
,左焦点为F(-1,0),
(1)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线L与椭圆C交于M,N两点,若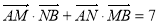 ,求直线L的方程;
,求直线L的方程;
(2)椭圆C上是否存在三点P,E,G,使得S△OPE=S△OPG=S△OEG=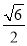 ?
?
(1) 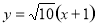 和
和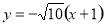 ; (2) 椭圆
; (2) 椭圆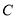 上不存在满足条件的三点
上不存在满足条件的三点
【解析】
试题分析:(1) 由已知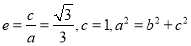 可解得
可解得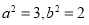 ,即椭圆方程为
,即椭圆方程为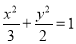 。可得
。可得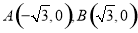 。根据点斜式可得直线
。根据点斜式可得直线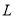 即直线
即直线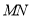 方程为
方程为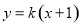 ,将直线方程和椭圆方程联立消去
,将直线方程和椭圆方程联立消去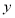 整理为关于
整理为关于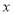 的一元二次方程,可得根与系数的关系。再根据
的一元二次方程,可得根与系数的关系。再根据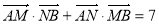 可求得
可求得 的值,即可得所求直线方程。 (2)根据两点确定一条直线可设
的值,即可得所求直线方程。 (2)根据两点确定一条直线可设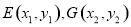 两点确定的直线为 l,注意讨论直线的斜率存在与否,用弦长公式可得
两点确定的直线为 l,注意讨论直线的斜率存在与否,用弦长公式可得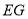 的长,用点到线的距离公式可得点
的长,用点到线的距离公式可得点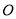 到线
到线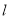 的距离,从而可得三角形面积。同理可得另两个三角形面积,联立方程可得三点横纵坐标的平方,根据三点坐标判断能否与点
的距离,从而可得三角形面积。同理可得另两个三角形面积,联立方程可得三点横纵坐标的平方,根据三点坐标判断能否与点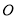 构成三角形,若能说明存在满足要求的三点否则说明不存在。
构成三角形,若能说明存在满足要求的三点否则说明不存在。
试题解析:(1)由题意:椭圆的方程为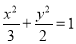 .
.
设点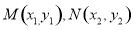 ,由
,由 得直线
得直线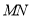 的方程为
的方程为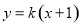 .
.
由方程组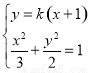 消去
消去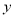 ,整理得
,整理得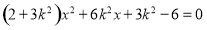 ,
,
可得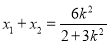 ,
,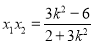 .
.
因为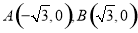 ,
,
所以
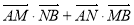
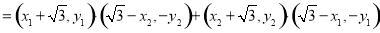
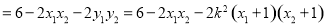
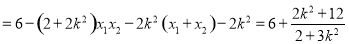
由已知得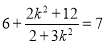 ,解得
,解得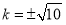 .
.
故所求直线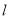 的方程为:
的方程为: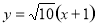 和
和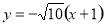
(2) 假设存在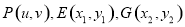 满足
满足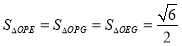 .
.
不妨设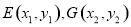 两点确定的直线为 l,
两点确定的直线为 l,
(ⅰ)当直线l的斜率不存在时, 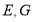 两点关于
两点关于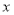 轴对称,
轴对称,
所以 ,
,
因为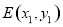 在椭圆上,
在椭圆上,
所以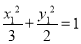 .①
.①
又因为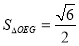 ,
,
所以|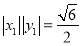 ,②
,②
由①、②得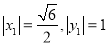 ,
,
此时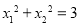 ,
,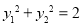 .
.
(ⅱ)当直线l的斜率存在时,设直线l的方程为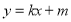 ,
,
由题意知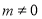 ,将其代入
,将其代入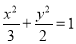 得
得
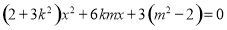 ,
,
其中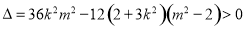 ,
,
即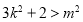 ,(★)
,(★)
又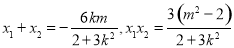 ,
,
所以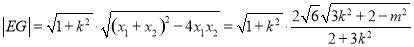 .
.
因为点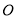 到直线l的距离为
到直线l的距离为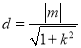 ,
,
所以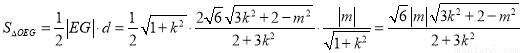 .
.
又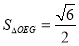 ,
,
整理得 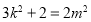 ,且符合(★)式.
,且符合(★)式.
此时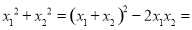
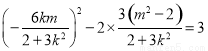 ,
,
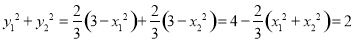 .
.
综上所述,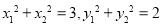 ,结论成立.
,结论成立.
同理可得: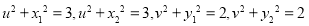 ,
,
解得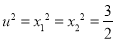 ;
;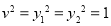 .
.
因此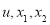 只能从
只能从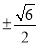 中选取,
中选取,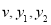 只能从
只能从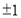 中选取.
中选取.
因此 只能在
只能在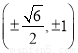 这四点中选取三个不同点,
这四点中选取三个不同点,
而这三点的两两连线中必有一条过原点,
与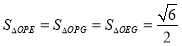 矛盾,
矛盾,
所以椭圆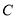 上不存在满足条件的三点
上不存在满足条件的三点
考点:1椭圆方程;2向量数量积公式;3直线和圆锥曲线的位置关系问题;4三角形面积问题。


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试理科数学试卷(解析版) 题型:选择题
为研究语文成绩和英语成绩之间是否具有线性相关关系,统计两科成绩得到如图所示的散点图(两坐标轴单位长度相同),用回归直线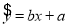 近似的刻画其相关关系,根据图形,以下结论最有可能成立的是( )
近似的刻画其相关关系,根据图形,以下结论最有可能成立的是( )

A.线性相关关系较强,b的值为1.25
B.线性相关关系较强,b的值为O.83
C.线性相关关系较强,b的值为-0.87
D.线性相关关系太弱,无研究价值
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)理科数学试卷(解析版) 题型:选择题
如果函数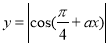 的图象关于直线
的图象关于直线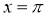 对称,则正实数
对称,则正实数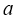 的最小值是( )
的最小值是( )
A.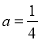 B.
B.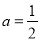 C.
C.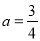 D.
D.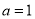
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)文科数学试卷(解析版) 题型:选择题
某程序框图如图所示,若该程序运行后输出的值是( )

A.2 B.-2 C.3 D.-3
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(三)理科数学试卷(解析版) 题型:选择题
在高校自主招生中,某学校获得5个推荐名额,其中清华大学2名,北京大学2名,复旦大学1名。并且北京大学和清华大学都要求必须有男生参加。学校通过选拔定下3男2女共5个推荐对象,则不同的推荐方法共有( )
(A)20种 (B)22种 (C)24种 (D)36种
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(三)文科数学试卷(解析版) 题型:填空题
已知PA垂直于正方形ABCD所在平面,连接PB、PC、PD、AC、BD,则下列垂直关系中正确的序号是 .
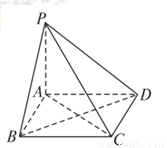
①平面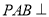 平面PBC ②平面
平面PBC ②平面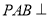 平面PAD ③平面
平面PAD ③平面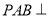 平面PCD
平面PCD
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省六市六校联盟高考模拟文科数学试卷(解析版) 题型:填空题
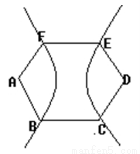
如图,正六边形ABCDEF的两个顶点A、D为双曲线的焦点,其余四个顶点都在双曲线上,则该双曲线的离心率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com