
分析 利用三次函数对称中心的定义和性质进行判断①③;分别求出函数f(x)=x3-3x2-3x+5与函数$y=tan\frac{π}{2}x$的对称中心判断②;求出函数$g(x)=\frac{1}{3}{x^3}-\frac{1}{2}{x^2}-\frac{5}{12}$的对称中心,可得g(x)+g(1-x)=-1,进一步求得$g(\frac{1}{2016})+g(\frac{2}{2016})+g(\frac{3}{2016})+…+g(\frac{2015}{2016})$=-1007.5判断④.
解答 解:∵任何三次函数的二阶导数都是一次函数,∴任何三次函数只有一个对称中心,故①不正确;
由f(x)=x3-3x2-3x+5,得f′(x)=3x2-6x-3,f″(x)=6x-6,由6x-6=0,得x=1,函数f(x)的对称中心为(1,0),
又由$\frac{π}{2}x=\frac{kπ}{2},k∈Z$,得x=k,k∈Z,∴f(x)的对称中心是函数$y=tan\frac{π}{2}x$的一个对称中心,故②正确;
∵任何三次函数都有对称中心,且“拐点”就是对称中心,
∴存在三次函数f′(x)=0有实数解x0,点(x0,f(x0))为y=f(x)的对称中心,即③正确;
∵$g(x)=\frac{1}{3}{x^3}-\frac{1}{2}{x^2}-\frac{5}{12}$,
∴g′(x)=x2-x,g''(x)=2x-1,
令g''(x)=2x-1=0,得x=$\frac{1}{2}$,
∵g($\frac{1}{2}$)=$\frac{1}{3}$×($\frac{1}{2}$)3-$\frac{1}{2}$×($\frac{1}{2}$)2-$\frac{5}{12}$=-$\frac{1}{2}$,
∴函数$g(x)=\frac{1}{3}{x^3}-\frac{1}{2}{x^2}-\frac{5}{12}$的对称中心是($\frac{1}{2}$,-$\frac{1}{2}$),
∴g(x)+g(1-x)=-1,
∴$g(\frac{1}{2016})+g(\frac{2}{2016})+g(\frac{3}{2016})+…+g(\frac{2015}{2016})$=-1007.5,故④正确.
故答案为:②③④.
点评 本题考查命题的真假判断与应用,主要考查函数与导数等知识,考查化归与转化的数学思想方法,考查化简计算能力,求函数的值以及函数的对称性的应用,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
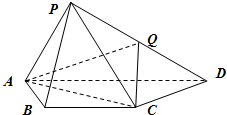 如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2$\sqrt{3}$,PA⊥PD,Q为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2$\sqrt{3}$,PA⊥PD,Q为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{π}{4},\frac{π}{3}})$ | B. | $({-\frac{π}{4},2})$ | C. | $({-1,\frac{π}{3}})$ | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
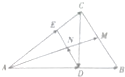 如图所示,在△ABC中,3$\overrightarrow{AD}=2\overrightarrow{AB}$,3$\overrightarrow{AE}=2\overrightarrow{AC}$,AM是BC边上的中线,且交DE于N,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.
如图所示,在△ABC中,3$\overrightarrow{AD}=2\overrightarrow{AB}$,3$\overrightarrow{AE}=2\overrightarrow{AC}$,AM是BC边上的中线,且交DE于N,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com